题目内容
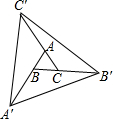如图，分别延长△ABC的三边AB、BC、CA至A′、B′、C′，使得AA′=3AB，BB′=3BC，CC′=3AC，若S△ABC=1，则S△A'B'C‘=
分析：由于AA′=3AB，且△ABC和△A′BC同高且底边在同一直线上，有三角形的面积公式可得
=
=
，
即：S△A′BC=2×S△ABC=2，同理可以求出其他部分的面积，最后求出总和，即是S△A′B′C′．
| S△ABC |
| S△A′BC |
| AB |
| A′B |
| 1 |
| 2 |
即：S△A′BC=2×S△ABC=2，同理可以求出其他部分的面积，最后求出总和，即是S△A′B′C′．
解答：
解：如下图所示：连接AB′，BC′，CA′
由三角形的面积公式且AA′=3AB，易知：
=
=
=
，
所以，S△A′BC=2×S△ABC=2，
同理可得：S△ABC′=S△AB′C=2，S△A′B′C=S△A′BC′=S△AB′C′=4，
所以，S△A′B′C′=S△ABC+S△A′BC+S△ABC′+S△AB′C+S△A′BC′+S△A′B′C+S△AB′C′
=1+2+2+2+4+4+4=19．
故答案为19．
解：如下图所示：连接AB′，BC′，CA′由三角形的面积公式且AA′=3AB，易知：
| S△ABC |
| S△A′BC |
| AB |
| A′B |
| AB |
| A′A-AB |
| 1 |
| 2 |
所以，S△A′BC=2×S△ABC=2，
同理可得：S△ABC′=S△AB′C=2，S△A′B′C=S△A′BC′=S△AB′C′=4，
所以，S△A′B′C′=S△ABC+S△A′BC+S△ABC′+S△AB′C+S△A′BC′+S△A′B′C+S△AB′C′
=1+2+2+2+4+4+4=19．
故答案为19．
点评：本题主要考查了灵活运用三角形的面积公式，求出各部分之间的关系，进而求出面积的方法．
练习册系列答案
七星图书口算速算天天练系列答案
相关题目
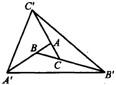4、如图，分别延长△ABC的三边AB，BC，CA至A′，B′，C′，使得AA′=3AB，BB′=3BC，CC′=3AC．若S△ABC=1，则S△A′B′C′等于（ ）
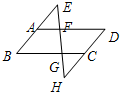19、如图，分别延长?ABCD的边BA、DC到点E、H，使得AE=AB，CH=CD，连接EH，分别交AD、BC于点F、G．
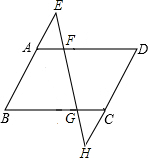如图，分别延长?ABCD的边BA、DC到点E、H，使得AE=AB，CH=CD，连接EH，分别交AD、BC于点F、G．
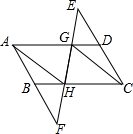如图，分别延长?ABCD的边CD，AB到E，F，使DE=BF，连接EF，分别交AD，BC于G，H，连结CG，AH．求证：CG∥AH．