Question

【题目】在一条东西走向河的一侧有一村庄，河边原有两个取水点，其中，由于某种原因，由到的路现在已经不通，该村为方便村民取水决定在河边新建一个取水点在同一条直线上)，并新修一条路，测得千米，千米，千米．

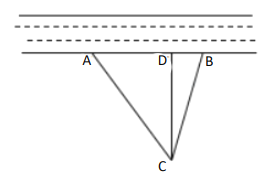
(1)问是否为从村庄到河边最近的路？请通过计算加以说明：

(2)求原来的路线的长．

Answer 1

【答案】(1)是，理由见解析； (2)原来的路线的长为千米

【解析】

（1）结合已知条件根据勾股定理的逆定理、垂直的定义、垂线段最短即可得解；

（2）设千米，则千米、千米，根据勾股定理列出关于的方程求解即可．

解：（1）结论：是从村庄到河边最近的路．

理由： ∵在中，千米，千米，千米

∴，即

∴是直角三角形

∴

∴

∴是从村庄到河边最近的路．

设千米，则千米，千米

∵在中，由勾股定理得：

∴

∴

答：原来的路线的长为千米．