题目内容
如图，点C是线段AB上的一个动点，AB=1，分别以AC和CB为一边作正方形，用S表示这两个正方形的面积之和，下列判断正确的是
- A.当C是AB的中点时，S最小
- B.当C是AB的中点时，S最大
- C.当C为AB的三等分点时，S最小
- D.当C为AB的三等分点时，S最大
A
分析：根据四个选择项，可知要判断的问题是C在AB的什么位置时，S有最大或最小值．由于点C是线段AB上的一个动点，可设AC=x，然后用含x的代数式表示S，得到S与x的函数关系式，最后根据函数的性质进行判断．
解答：设AC=x，则CB=1-x，
S=x2+（1-x）2即S=2x2-2x+1，
所以当x=
=
时，S最小．
此时，C是AB的中点．
故选A．
点评：此类题目涉及到最值，它的解决需建立二次函数的关系式，然后利用抛物线的顶点公式求解．
分析：根据四个选择项，可知要判断的问题是C在AB的什么位置时，S有最大或最小值．由于点C是线段AB上的一个动点，可设AC=x，然后用含x的代数式表示S，得到S与x的函数关系式，最后根据函数的性质进行判断．
解答：设AC=x，则CB=1-x，
S=x2+（1-x）2即S=2x2-2x+1，
所以当x=
=时，S最小．此时，C是AB的中点．
故选A．
点评：此类题目涉及到最值，它的解决需建立二次函数的关系式，然后利用抛物线的顶点公式求解．
练习册系列答案
应用题天天练四川大学出版社系列答案
相关题目
如图，点C是线段AB的中点，点D是线段BC的中点，下面等式不正确的是（ ）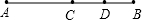
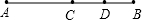
| A、CD=AD-BC | ||
| B、CD=AC-DB | ||
C、CD=
| ||
D、CD=
|
10、如图，点D是线段AB与线段BC的垂直平分线的交点，∠B=40°，则∠ADC等于（ ）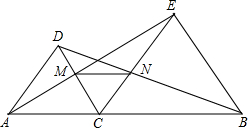
AC、BC为边在直线AB的同侧作等边△ACD和等边△BCE，AE与CD相交于点M，BD和CE相交于点N．
如图，点C是线段AB的中点，点D是线段CB上任意一点，则下列表示线段关系的式子不正确的是（ ）
如图，点C是线段AB的中点，点D是线段BC的中点，则下列结论中错误的是（ ）