题目内容
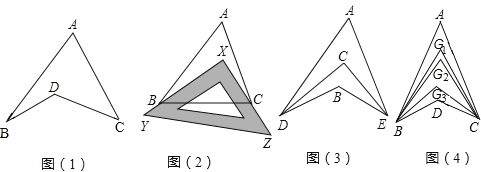
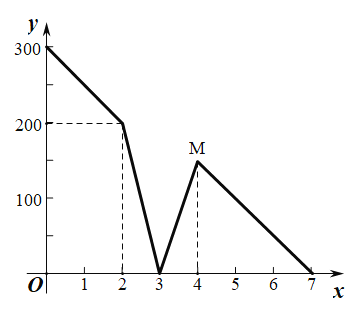
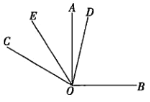
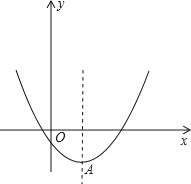
【题目】如图,已知![]() ,
,![]() 于
于![]() ,
,![]() 为
为![]() 中点,连接
中点,连接![]() ,将
,将![]() 向右平移到
向右平移到![]() ,使
,使![]() 与
与![]() 重合,
重合,![]() 与
与![]() 重合,
重合,![]() 与
与![]() 重合,连接
重合,连接![]() ,
,![]() ,
,![]() ,若
,若![]() 为
为![]() 的高的交点,
的高的交点,![]() ,
,![]() ,则
,则![]() 到
到![]() 的距离为________.
的距离为________.
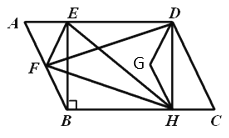
【答案】3
【解析】
延长HG交FD于N点,过F点作FM⊥EH,由直角三角形斜边中线性质得AF=EF=BF,利用平移、等腰三角形性质、垂直等条件证明角相等从而可得![]() ,根据相似三角形性质求出AF长,再由勾股定理即可求出BE、FD、EH等线段长,有勾股定理逆定理证明
,根据相似三角形性质求出AF长,再由勾股定理即可求出BE、FD、EH等线段长,有勾股定理逆定理证明![]() 是直角三角形,从而由三角形面积求出斜边的高.
是直角三角形,从而由三角形面积求出斜边的高.
解:延长HG交FD于N点,过F点作FM⊥EH,
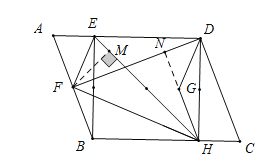
∵![]() 于
于![]() ,即∠BED=∠EBH=90°,
,即∠BED=∠EBH=90°,![]() 为
为![]() 中点,
中点,
∴AF=EF=BF,
∴∠FEB=∠FBE,∠FAE=∠FEA,
由平移性质可知:∠HDE=∠DHB=90°,∠GHD=∠GDH=∠FEB=∠FBE,∠AEF=∠GDA,
∴四边形BHDE是矩形,
∴BH=DE=8,
∵![]() 为
为![]() 的高的交点,
的高的交点,
∴∠GHD+∠FDH=90°,
又∵∠FDH+∠FDA=90°,
∴∠FDA=∠GHD,
∴∠FDA=∠ABE,
∴∠AFD=∠AEB=90°,
又∵∠A=∠A,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,
∴![]()
∴在![]() 中,
中,![]()
在![]() 中,
中,![]()
在![]() 中,
中,![]()
易证![]()
∴在![]() 中
中![]() ,
,
∴![]() 是直角三角形,∠EFH=90°,
是直角三角形,∠EFH=90°,
∴![]() ,即
,即![]() ,
,
∴![]() .即
.即![]() 到
到![]() 的距离为3.
的距离为3.
故答案为:3.

练习册系列答案
相关题目