题目内容
设x为一切实数,则下列等式一定成立的是
- A.
 =x
=x - B.
 =1
=1 - C.x-|x|=0
- D.
 =-x
=-x
D
分析:A、根据二次根式的性质即可判定;
B、根据分式的定义即可判定;
C、根据绝对值的定义即可判定;
D、根据立方根的定义即可判定.
解答:A、当x<0时, =x不成立,故选项错误;
=x不成立,故选项错误;
B、当x=0时 =1不成立,故选项错误;
=1不成立,故选项错误;
C、当x<0时,x-|x|=x+x=2x,故选项错误;
D、无论x为何值, =-x总是成立,故选项正确.
=-x总是成立,故选项正确.
故选D.
点评:此题主要考查了实数的各种不同形式的性质.解决这类问题,一般的方法是举出反例,能举出范例的则不成立.用字母代表的代数式一定要考虑字母的取值范围.
分析:A、根据二次根式的性质即可判定;
B、根据分式的定义即可判定;
C、根据绝对值的定义即可判定;
D、根据立方根的定义即可判定.
解答:A、当x<0时,
 =x不成立,故选项错误;
=x不成立,故选项错误;B、当x=0时
 =1不成立,故选项错误;
=1不成立,故选项错误;C、当x<0时,x-|x|=x+x=2x,故选项错误;
D、无论x为何值,
 =-x总是成立,故选项正确.
=-x总是成立,故选项正确.故选D.
点评:此题主要考查了实数的各种不同形式的性质.解决这类问题,一般的方法是举出反例,能举出范例的则不成立.用字母代表的代数式一定要考虑字母的取值范围.

练习册系列答案
相关题目
 ,
, ,7xy+y3,
,7xy+y3, ,
, ,
, 中是分式的有
中是分式的有 =
=
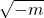



 ,其中分式的个数为
,其中分式的个数为
 的是
的是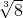 =2
=2 计算正确的是
计算正确的是
