题目内容
如图,已知平行四边形ABCD的顶点A的坐标是(0,8),AB平行于x轴,B,C,D三点 在抛物线y=
在抛物线y=| 9 |
| 16 |
| 75 |
| 2 |
(1)求出B,D两点的坐标;
(2)求a的值;
(3)作△ADN的内切圆⊙P,切点分别为M,K,H,求tan∠PFM的值.
分析:(1)已知了抛物线的解析式,而B的纵坐标就是A点的纵坐标,可代入抛物线的解析式中即可求出B点的坐标,也就知道了AB的长,由于四边形ABCD是平行四边形,因此AB=CD,根据抛物线的对称性,即可求出D点的横坐标.然后代入抛物线的解析式中即可得出D点的坐标;
(2)先根据E点坐标表示出直线上OE的解析式,进而求出F点的坐标.在梯形ADFE中,上下底的长就可求出,高是AN即A、D两点纵坐标的差,然后可根据梯形ADFE的面积求出a的值.
(3)求∠PFM的正切值,就要构建直角三角形,连接PM,PK,直角三角形PMN中,已知了FN的长(根据F点坐标可求得),而MN=PM=r,因此求出圆P的半径是关键.△ADN中,根据A、D两点的坐标即可求出AD、AN、DN的长.由于圆P内切于△ADN,因此可根据三角形内切圆半径公式求出圆P的半径.进而可在直角三角形PMF中,根据tan∠PFM=r:(r+FN)求出∠PFM的正切值.
(2)先根据E点坐标表示出直线上OE的解析式,进而求出F点的坐标.在梯形ADFE中,上下底的长就可求出,高是AN即A、D两点纵坐标的差,然后可根据梯形ADFE的面积求出a的值.
(3)求∠PFM的正切值,就要构建直角三角形,连接PM,PK,直角三角形PMN中,已知了FN的长(根据F点坐标可求得),而MN=PM=r,因此求出圆P的半径是关键.△ADN中,根据A、D两点的坐标即可求出AD、AN、DN的长.由于圆P内切于△ADN,因此可根据三角形内切圆半径公式求出圆P的半径.进而可在直角三角形PMF中,根据tan∠PFM=r:(r+FN)求出∠PFM的正切值.
解答: 解:(1)∵点A的坐标为(0,8),且AB∥x轴
解:(1)∵点A的坐标为(0,8),且AB∥x轴
∴B点纵坐标为8,且B点在抛物线y=
x2上
∴点B的坐标为(
,8)
∴AB=
又∵点D、C在抛物线y=
x2上,且CD∥x轴
∴D、C两点关于y轴对称
∴DN=CN=
∴D点的坐标为(-
,2).
(2)设E点的坐标为(a,8),则直线OE的解析式为:y=
x
∴F点的坐标为(
,2 )
由AE=a,DF=
+
且S四边形ADFE=
,
解得a=10-
.
(3)连接PH,PM,PK
∵⊙P是△AND的内切圆,H,M,K为切点
∴PH⊥AD PM⊥DN PK⊥AN
在Rt△AND中,由DN=
,AN=6,由勾股定理,得
AD=
设⊙P的半径为r,则
S△AND=
(
+
+6)r=
×6×
,r=
在正方形PMNK中,PM=MN=
∴MF=MN+NF=
+
-
在Rt△PMF中,tan∠PFM=
=
.
 解:(1)∵点A的坐标为(0,8),且AB∥x轴
解:(1)∵点A的坐标为(0,8),且AB∥x轴∴B点纵坐标为8,且B点在抛物线y=
| 9 |
| 16 |
∴点B的坐标为(
8
| ||
| 3 |
∴AB=
8
| ||
| 3 |
又∵点D、C在抛物线y=
| 9 |
| 16 |
∴D、C两点关于y轴对称
∴DN=CN=
4
| ||
| 3 |
∴D点的坐标为(-
4
| ||
| 3 |
(2)设E点的坐标为(a,8),则直线OE的解析式为:y=
| 8 |
| a |
∴F点的坐标为(
| a |
| 4 |
由AE=a,DF=
4
| ||
| 3 |
| a |
| 4 |
| 75 |
| 2 |
解得a=10-
4
| ||
| 5 |
(3)连接PH,PM,PK
∵⊙P是△AND的内切圆,H,M,K为切点
∴PH⊥AD PM⊥DN PK⊥AN
在Rt△AND中,由DN=
4
| ||
| 3 |
AD=
2
| ||
| 3 |
设⊙P的半径为r,则
S△AND=
| 1 |
| 2 |
4
| ||
| 3 |
2
| ||
| 3 |
| 1 |
| 2 |
4
| ||
| 3 |
12
| ||||
2
|
在正方形PMNK中,PM=MN=
12
| ||||
2
|
∴MF=MN+NF=
12
| ||||
2
|
| 5 |
| 2 |
| ||
| 5 |
在Rt△PMF中,tan∠PFM=
| PM |
| MF |
| ||||||||||||||
|
点评:本题是二次函数的综合题,考查了三角形的内切圆,解直角三角形,平行四边形的性质,二次函数的性质等知识点,综合性较强,考查学生数形结合的数学思想方法.

练习册系列答案
相关题目
 CD的边长a等于点P,Q间的距离.
CD的边长a等于点P,Q间的距离. 如图,已知平行四边形ABCD的对角线AC,BD相交于点O,BD绕点O顺时针旋转交AB,DC于E,F.
如图,已知平行四边形ABCD的对角线AC,BD相交于点O,BD绕点O顺时针旋转交AB,DC于E,F.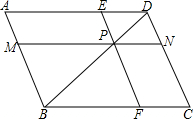 交AB、CD、AD、BC于M、N、E、F,设a=PM•PE,b=PN•PF.
交AB、CD、AD、BC于M、N、E、F,设a=PM•PE,b=PN•PF. 23、如图,已知平行四边形ABCD.
23、如图,已知平行四边形ABCD. 如图,已知平行四边形ABCD,作DE⊥AB,垂足为E,把三角形AED沿AB方向平移AB长个单位长度.
如图,已知平行四边形ABCD,作DE⊥AB,垂足为E,把三角形AED沿AB方向平移AB长个单位长度.