Question

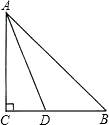在Rt△ABC中，∠C=90°，若AB=20，AC=16，AD平分∠BAC交BC于点D，则点D到线段AB的距离为

3

．

Answer 1

分析：利用勾股定理列式求出BC的长，再求出CD的长，过点D作DE⊥AB于E，然后根据角平分线上的点到角的两边的距离相等可得DE=CD．

解答：解：∵∠C=90°，AB=20，AC=16，
∴BC=

AB2-AC2

=

202-162

=12，
∵BD：CD=3：1，
∴CD=12×

1

1+3

=3，
∵AD平分∠BAC，
∴DE=CD=3，
即点D到线段AB的距离为3．
故答案为：3．

点评：本题考查了角平分线上的点到角的两边的距离相等的性质，熟记性质是解题的关键．