题目内容
已知直角三角形的两直角边的长恰好是方程x2-7x+12=0的两根，则此直角三角形斜边上中线的长为________．
2.5
分析：解用因式分解法一元二次方程可得x的两个解，已知直角三角形的两直角边根据勾股定理计算斜边长，根据斜边中线长为斜边的一半计算斜边中线长．
解答：直角三角形两直角边为x2-7x+12=0的两个解，
x2-7x+12=0，∵7=3+4，12=3×4，
∴x2-7x+12=（x-3）（x-4）=0．
故x的两个解为3，4，
根据勾股定理斜边长=
=5，
故斜边中线长为
×5=2.5
故答案为 2.5．
点评：本题考查了直角三角形中勾股定理的运用，考查了因式分解法计算一元二次方程的根，考查了斜边中线为斜边长的一半的性质，本题中正确的运用因式分解法计算x2-7x+12=0的根是解题的关键．
分析：解用因式分解法一元二次方程可得x的两个解，已知直角三角形的两直角边根据勾股定理计算斜边长，根据斜边中线长为斜边的一半计算斜边中线长．
解答：直角三角形两直角边为x2-7x+12=0的两个解，
x2-7x+12=0，∵7=3+4，12=3×4，
∴x2-7x+12=（x-3）（x-4）=0．
故x的两个解为3，4，
根据勾股定理斜边长=
=5，故斜边中线长为
×5=2.5故答案为 2.5．
点评：本题考查了直角三角形中勾股定理的运用，考查了因式分解法计算一元二次方程的根，考查了斜边中线为斜边长的一半的性质，本题中正确的运用因式分解法计算x2-7x+12=0的根是解题的关键．
练习册系列答案
相关题目
学习过三角函数，我们知道在直角三角形中，一个锐角的大小与两条边长的比值相互唯一确定，因此边长与角的大小之间可以相互转化．类似的，也可以在等腰三角形中建立边角之间的联系，我们定义：等腰三角形中底边与腰的比叫做顶角的正对（sad）．如图，在△ABC中，AB=AC，顶角A的正对记作sadA，这时sad A=
学习过三角函数，我们知道在直角三角形中，一个锐角的大小与两条边长的比值相互唯一确定，因此边长与角的大小之间可以相互转化．类似的，也可以在等腰三角形中建立边角之间的联系，我们定义：等腰三角形中底边与腰的比叫做顶角的正对（sad）．如图，在△ABC中，AB=AC，顶角A的正对记作sadA，这时sad A=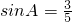
，其中A为锐角，试求sadA的值；