Question

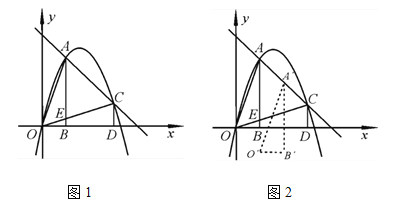
【题目】已知，直线与双曲线交于点，点.

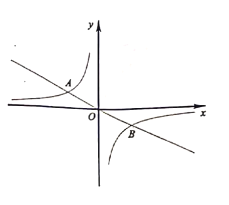
（1）求反比例函数的表达式；

（2）根据图象直接写出不等式的解集 .

（3）将直线沿轴向下平移后，分别与轴，轴交于点，点，当四边形为平行四边形时，求直线的表达式.

Answer 1

【答案】（1）；（2）或；（3）,

【解析】

（1）将点A代入直线解析式即可得出其坐标，再代入反比例函数解析式，即可得解；

（2）首先联立两个函数，解得即可得出点B坐标，直接观察图像，即可得出解集；

（3）首先过点作轴，过点作轴，交于点，根据平行线的性质，得出，得出，进而得出直线CD解析式.

解：（1）根据题意，可得点

将其代入反比例函数解析式，即得

（2）根据题意，得

解得

∴点B（4，-2）

∴直接观察图像，可得的解集为

或

（3）过点作轴，过点作轴，交于点

根据题意，可得

∴∠EAB=∠NOB=∠OCD，∠AEB=∠COD=90°，AB=CD

∴∠ABE=∠CDO

∴（ASA）

∴

则可得出直线CD为