题目内容
已知抛物线过点A(2,0),B(-1,0),与y轴交于点C,且OC=2.则这条抛物线的解析式为
- A.y=x2-x-2
- B.y=-x2+x+2
- C.y=x2-x-2或y=-x2+x+2
- D.y=-x2-x-2或y=x2+x+2
C
分析:首先由OC=2,可知C点的坐标是(0,2)或(0,-2),然后分别把A、B、C三点的坐标代入函数的解析式,用待定系数法求出.注意本题有两种情况.
解答:抛物线与y轴交于点C,且OC=2,则C点的坐标是(0,2)或(0,-2),
当C点坐标是(0,2)时,图象经过三点,可以设函数解析式是:y=ax2+bx+c,
把(2,0),(-1,0),(0,2)分别代入解析式,
得到: ,
,
解得: ,
,
则函数解析式是:y=-x2+x+2;
同理可以求得当C是(0,-2)时解析式是:y=x2-x-2.
故这条抛物线的解析式为:y=-x2+x+2或y=x2-x-2.
故选C.
点评:求函数解析式的方法就是待定系数法,转化为解方程组的问题,这是求解析式常用的方法.
分析:首先由OC=2,可知C点的坐标是(0,2)或(0,-2),然后分别把A、B、C三点的坐标代入函数的解析式,用待定系数法求出.注意本题有两种情况.
解答:抛物线与y轴交于点C,且OC=2,则C点的坐标是(0,2)或(0,-2),
当C点坐标是(0,2)时,图象经过三点,可以设函数解析式是:y=ax2+bx+c,
把(2,0),(-1,0),(0,2)分别代入解析式,
得到:
 ,
,解得:
 ,
,则函数解析式是:y=-x2+x+2;
同理可以求得当C是(0,-2)时解析式是:y=x2-x-2.
故这条抛物线的解析式为:y=-x2+x+2或y=x2-x-2.
故选C.
点评:求函数解析式的方法就是待定系数法,转化为解方程组的问题,这是求解析式常用的方法.

练习册系列答案
 期末集结号系列答案
期末集结号系列答案
相关题目
已知抛物线过点A(2,0),B(-1,0),与y轴交于点C,且OC=2.则这条抛物线的解析式为( )
| A、y=x2-x-2 | B、y=-x2+x+2 | C、y=x2-x-2或y=-x2+x+2 | D、y=-x2-x-2或y=x2+x+2 |
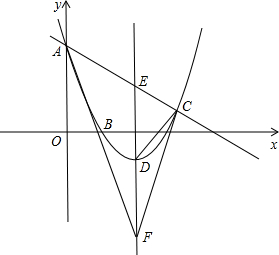 如图,已知抛物线过点A(0,6),B(2,0),C(7,
如图,已知抛物线过点A(0,6),B(2,0),C(7,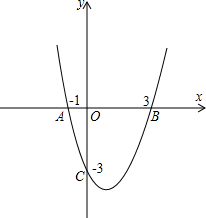 如图,已知抛物线过点A(-1,0)、B(3,0)、C(0,-3).
如图,已知抛物线过点A(-1,0)、B(3,0)、C(0,-3).