题目内容
如图,矩形纸片ABDC中,AB=5,AC=3,将纸片折叠,使点B落在边CD上的B′处,折痕为AE.在折痕A E上存在一点P到边CD的距离与到点B的距离相等,则此相等距离为__________.

【答案】
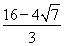 .
.
【解析】
试题分析:先根据题意画出图形,由翻折变换的性质得出F、B′重合,分别延长AE,CD相交于点G,由平行线的性质可得出GB′=AB′=AB=4,再根据相似三角形的判定定理得出△ACG∽△PB′G,求出其相似比,进而可求出答案.
试题解析:如图所示,设PF⊥CD,
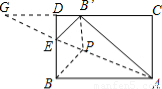
由翻折变换的性质可得BP=B′P,
又∵P到边CD的距离与到点B的距离相等,
∴B'P⊥CD,
∵AB平行于CD,
∴∠BAG=∠AGC,
∵∠BAG=∠B′AG,AGC=∠B′AG,
∴GB′=AB′=AB=4,
∵PB′⊥CD,
∴PB′∥AC,
∴△ACG∽△PB′G,
∵Rt△ADB′中,AB′=4,AC=3,
∴CB′=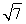 ,
,
在△ACG和△PB′G中.
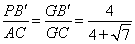 ,
,
解得:PB'=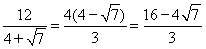
考点: 1.翻折变换(折叠问题);2.勾股定理;3.矩形的性质.

练习册系列答案
相关题目
 29、如图,矩形纸片ABCD,AB=2,∠ADB=30°,沿对角线BD折叠(使△ABD和△EBD落在同一平面内),则A、E两点间的距离为
29、如图,矩形纸片ABCD,AB=2,∠ADB=30°,沿对角线BD折叠(使△ABD和△EBD落在同一平面内),则A、E两点间的距离为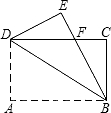 如图,矩形纸片ABCD,BC=2,∠ABD=30度.将该纸片沿对角线BD翻折,点A落在点E处,EB交DC于点F,则点F到直线DB的距离为
如图,矩形纸片ABCD,BC=2,∠ABD=30度.将该纸片沿对角线BD翻折,点A落在点E处,EB交DC于点F,则点F到直线DB的距离为 如图,矩形纸片ABCD,BC=2
如图,矩形纸片ABCD,BC=2 如图,矩形纸片ABCD,AB=2,∠ADB=30°,沿对角线BD折叠(使△ABD和△EBD落在同一平面内),求A、E两点间的距离.
如图,矩形纸片ABCD,AB=2,∠ADB=30°,沿对角线BD折叠(使△ABD和△EBD落在同一平面内),求A、E两点间的距离.