题目内容
 如图,等腰梯形ABCD中,AD∥BC,BC=4AD=
如图,等腰梯形ABCD中,AD∥BC,BC=4AD= ,∠B=45°,直角三角尺含45°角的顶点E在边BC上移动,一直角边始终经过点A,斜边交CD于点F.若△ABE为等腰三角形,求CF的长.
,∠B=45°,直角三角尺含45°角的顶点E在边BC上移动,一直角边始终经过点A,斜边交CD于点F.若△ABE为等腰三角形,求CF的长.
解:如图,过点A作AM⊥BC于M,过点D作DN⊥BC于N,
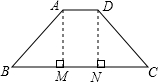
∵等腰梯形ABCD中,AD∥BC,BC=4AD=4 ,
,
∴BM= (BC-AD)=
(BC-AD)= (4
(4 -
- )=
)= ,∠C=∠B=45°,
,∠C=∠B=45°,
∵∠B=45°,
∴AB= BM=
BM= ×
× =3,
=3,
①如图1,AE=BE时,∵∠B=45°,
∴∠BAE=∠B=45°,
∴△ABE是等腰直角三角形,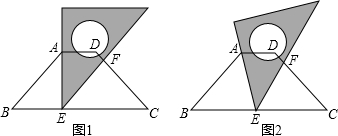
∴BE= AB=
AB= ,
,
∴CE=BC-BE=4 -
- =
= ,
,
又∵∠CEF=180°-∠AEB-∠AEF=180°-90°-45°=45°,
∴△CEF是等腰直角三角形,
∴CF= CE=
CE= ×
× =
= ;
;
②如图2,AB=BE时,∵∠B=45°,
∴∠AEB= (180°-∠B)=
(180°-∠B)= (180°-45°)=67.5°,
(180°-45°)=67.5°,
∴∠CEF=180°-∠AEB-∠AEF=180°-67.5°-45°=67.5°,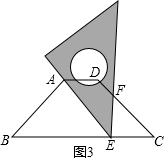
∴∠CFE=180°-∠C-∠CEF=180°-45°-67.5°=67.5°,
∴∠CEF=∠CFE,
∴CF=CE,
∵BC=4 ,AB=3,
,AB=3,
∴CF=CE=BC-BE=4 -3;
-3;
③如图3,AB=AE时,∠AEB=∠B=45°,
∴∠CEF=180°-∠AEB-∠AEF=180°-45°-45°=90°,
∴△ABE、△CEF都是等腰直角三角形,
∴BE= AB=3
AB=3 ,
,
CE=BC-BE=4 -3
-3 =
= ,
,
∴CF= CE=
CE= ×
× =2;
=2;
综上所述,CF的长为 或4
或4 -3或2.
-3或2.
分析:过点A作AM⊥BC于M,过点D作DN⊥BC于N,根据等腰三角形的性质求出BM的长度,再求出AB,然后分①AE=BE时,△ABE、△CEF都是等腰直角三角形,求出BE的长,再求出CE的长,然后根据局等腰直角三角形的性质求解即可;②AB=BE时,先求出CE的长度,再求出∠AEB的度数,再根据平角等于180°求出∠CEF,然后求出∠CFE,根据度数得到∠CEF=∠CFE,根据等角对等边的性质可得CF=CE;③AB=AE时,判断出△ABE、△CEF都是等腰直角三角形,然后根据等腰直角三角形的性质求解即可.
点评:本题考查了等腰梯形的性质,等腰直角三角形的性质,熟记性质是解题的关键,难点在于根据腰长的不同,分情况讨论.

∵等腰梯形ABCD中,AD∥BC,BC=4AD=4
 ,
,∴BM=
 (BC-AD)=
(BC-AD)= (4
(4 -
- )=
)= ,∠C=∠B=45°,
,∠C=∠B=45°,∵∠B=45°,
∴AB=
 BM=
BM= ×
× =3,
=3,①如图1,AE=BE时,∵∠B=45°,
∴∠BAE=∠B=45°,
∴△ABE是等腰直角三角形,

∴BE=
 AB=
AB= ,
,∴CE=BC-BE=4
 -
- =
= ,
,又∵∠CEF=180°-∠AEB-∠AEF=180°-90°-45°=45°,
∴△CEF是等腰直角三角形,
∴CF=
 CE=
CE= ×
× =
= ;
;②如图2,AB=BE时,∵∠B=45°,
∴∠AEB=
 (180°-∠B)=
(180°-∠B)= (180°-45°)=67.5°,
(180°-45°)=67.5°,∴∠CEF=180°-∠AEB-∠AEF=180°-67.5°-45°=67.5°,

∴∠CFE=180°-∠C-∠CEF=180°-45°-67.5°=67.5°,
∴∠CEF=∠CFE,
∴CF=CE,
∵BC=4
 ,AB=3,
,AB=3,∴CF=CE=BC-BE=4
 -3;
-3;③如图3,AB=AE时,∠AEB=∠B=45°,
∴∠CEF=180°-∠AEB-∠AEF=180°-45°-45°=90°,
∴△ABE、△CEF都是等腰直角三角形,
∴BE=
 AB=3
AB=3 ,
,CE=BC-BE=4
 -3
-3 =
= ,
,∴CF=
 CE=
CE= ×
× =2;
=2;综上所述,CF的长为
 或4
或4 -3或2.
-3或2.分析:过点A作AM⊥BC于M,过点D作DN⊥BC于N,根据等腰三角形的性质求出BM的长度,再求出AB,然后分①AE=BE时,△ABE、△CEF都是等腰直角三角形,求出BE的长,再求出CE的长,然后根据局等腰直角三角形的性质求解即可;②AB=BE时,先求出CE的长度,再求出∠AEB的度数,再根据平角等于180°求出∠CEF,然后求出∠CFE,根据度数得到∠CEF=∠CFE,根据等角对等边的性质可得CF=CE;③AB=AE时,判断出△ABE、△CEF都是等腰直角三角形,然后根据等腰直角三角形的性质求解即可.
点评:本题考查了等腰梯形的性质,等腰直角三角形的性质,熟记性质是解题的关键,难点在于根据腰长的不同,分情况讨论.

练习册系列答案
相关题目
 14、如图,等腰梯形ABCD中,AB∥CD,∠A=60°,BD平分∠ABC,若梯形ABCD的周长为40cm,则CD的长为( )
14、如图,等腰梯形ABCD中,AB∥CD,∠A=60°,BD平分∠ABC,若梯形ABCD的周长为40cm,则CD的长为( ) 24、已知:如图,等腰梯形ABCD中,AD∥BC,BD平分∠ABC.
24、已知:如图,等腰梯形ABCD中,AD∥BC,BD平分∠ABC. (2007•昌平区二模)已知:如图,等腰梯形ABCD中,AD∥BC,BD平分∠ABC,∠A=120°,BD=
(2007•昌平区二模)已知:如图,等腰梯形ABCD中,AD∥BC,BD平分∠ABC,∠A=120°,BD= 如图,等腰梯形ABCD中,AD∥BC,AB=CD,对角线BD平分∠ABC,且BD⊥DC,上底AD=3cm.
如图,等腰梯形ABCD中,AD∥BC,AB=CD,对角线BD平分∠ABC,且BD⊥DC,上底AD=3cm. 如图,等腰梯形ABCD中,AD∥BC,AB=CD,BD平分∠ABC,BD⊥DC,延长BC到E,使CE=AD.
如图,等腰梯形ABCD中,AD∥BC,AB=CD,BD平分∠ABC,BD⊥DC,延长BC到E,使CE=AD.