题目内容
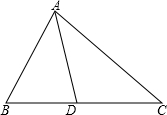
21、已知：如图△ABC中，AB=AC，∠C=30°，AB⊥AD，AD=4cm．求BC的长．分析：等腰△ABC中，根据∠B=∠C=30°，∠BAD=90°；易证得∠DAC=∠C=30°，即CD=AD=4cm．Rt△ABD中，根据30°角所对直角边等于斜边的一半，可求得BD=2AD=8cm；由此可求得BC的长．
解答：解：∵AB=AC
∴∠B=∠C=30°（1分）
∵AB⊥AD
∴BD=2AD=2×4=8（cm）（2分）
∠B+∠ADB=90°，
∴∠ADB=60°（3分）
∵∠ADB=∠DAC+∠C=60°
∴∠DAC=30°
∴∠DAC=∠C（4分）
∴DC=AD=4cm（5分）
∴BC=BD+DC=8+4=12（cm）．（6分）
∴∠B=∠C=30°（1分）
∵AB⊥AD
∴BD=2AD=2×4=8（cm）（2分）
∠B+∠ADB=90°，
∴∠ADB=60°（3分）
∵∠ADB=∠DAC+∠C=60°
∴∠DAC=30°
∴∠DAC=∠C（4分）
∴DC=AD=4cm（5分）
∴BC=BD+DC=8+4=12（cm）．（6分）
点评：主要考查：等腰三角形的性质、三角形内角和定理、直角三角形的性质．
练习册系列答案
相关题目
已知，如图△ABC中，AD为△ABC的角平分线，求证：AB•DC=AC•BD．
（1998•河北）已知：如图△ABC中，∠A的平分线AD交BC于D，⊙O过点A，且与BC相切于D，与AB、AC分别相交于E、F，AD与EF相交于G．
已知：如图△ABC中，∠ACB=90°，D是AC上任意一点，DE⊥AB于E，M，N分别是BD，CE的中点，求证：MN⊥CE．
已知，如图△ABC中，AB=AC，CD⊥AD于D，CD=
已知，如图△ABC中，D、E、F分别是三角形三边中点，△ABC的周长为30，面积为48，则△DEF的周长为