Question

【题目】小明在求同一坐标轴上两点间的距离时发现，对于平面直角坐标系内任意两点P1（x1，y1），P2（x2，y2），可通过构造直角三角形利用勾股定理得到结论：P1P2=；他还证明了线段P1P2的中点P（x，y）的坐标公式是：x=，y=；

启发应用

请利用上面的信息，解答下面的问题：

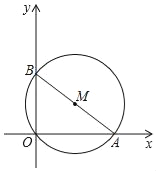
如图，在平面直角坐标系中，已知A（8，0），B（0，6），C（1，7），⊙M经过原点O及点A、B．

（1）求⊙M的半径及圆心M的坐标；

（2）判断点C与⊙M的位置关系，并说明理由．

Answer 1

【答案】（1）5，M（4，3）;(2)见解析.

【解析】

根据圆周角定理∠AOB=90°得AB为⊙M的直径，则可得到线段AB的中点即点M的坐标，然后利用勾股定理计算出AB=10，则可确定⊙M的半径为5；

求出CM=5和圆M的半径比较大小，即可得出结论.

解：（1）∵∠AOB=90°，

∴AB是⊙M的直径，

∵A（8，0），B（0，6），

∴AB= =10，

∴⊙M的半径为5，

由线段中点坐标公式x= ，y= ，得x=4，y=3，

∴M（4，3）;

（2）点C在⊙M上，

理由：∵C（1，7），M（4，3），

∴CM= =5，

∴点C在⊙M上．