题目内容
(2013•河南模拟)如图,在锐角△ABC中,AB=4,BC=5,∠ACB=45°,将△ABC绕点B按逆时针方向旋转,得到△A1BC1.
(1)如图1,当点C1在线段CA的延长线上时,求∠CC1A1的度数;
(2)如图2,连结AA1,CC1.若△ABA1的面积为4,求△CBC1的面积.
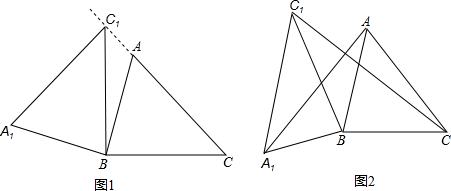
(1)如图1,当点C1在线段CA的延长线上时,求∠CC1A1的度数;
(2)如图2,连结AA1,CC1.若△ABA1的面积为4,求△CBC1的面积.

分析:(1)先由旋转的性质得出∠A1C1B=∠ACB=45°,BC=BC1,再根据等边对等角得出∠CC1B=∠C1CB=45°,则∠CC1A1=∠CC1B+∠A1C1B=90°;
(2)先由旋转的性质得出△ABC≌△A1BC1,则BA=BA1,BC=BC1,∠ABC=∠A1BC1,再根据两边对应成比例且夹角相等的两三角形相似证明△ABA1∽△CBC1,然后根据相似三角形的面积比等于相似比的平方即可求解.
(2)先由旋转的性质得出△ABC≌△A1BC1,则BA=BA1,BC=BC1,∠ABC=∠A1BC1,再根据两边对应成比例且夹角相等的两三角形相似证明△ABA1∽△CBC1,然后根据相似三角形的面积比等于相似比的平方即可求解.
解答: 解:(1)∵将△ABC绕点B按逆时针方向旋转,得到△A1BC1,
解:(1)∵将△ABC绕点B按逆时针方向旋转,得到△A1BC1,
∴∠A1C1B=∠ACB=45°,BC=BC1,
∴∠CC1B=∠C1CB=45°,
∴∠CC1A1=∠CC1B+∠A1C1B=45°+45°=90°;
(2)∵△ABC≌△A1BC1,
∴BA=BA1,BC=BC1,∠ABC=∠A1BC1,
∴
=
,∠ABC+∠ABC1=∠A1BC1+∠ABC1,
∴∠ABA1=∠CBC1,
∴△ABA1∽△CBC1,
∴
=(
)2=(
)2=
,
∵S△ABA1=4,
∴S△CBC1=
.
 解:(1)∵将△ABC绕点B按逆时针方向旋转,得到△A1BC1,
解:(1)∵将△ABC绕点B按逆时针方向旋转,得到△A1BC1,∴∠A1C1B=∠ACB=45°,BC=BC1,
∴∠CC1B=∠C1CB=45°,
∴∠CC1A1=∠CC1B+∠A1C1B=45°+45°=90°;
(2)∵△ABC≌△A1BC1,
∴BA=BA1,BC=BC1,∠ABC=∠A1BC1,
∴
| BA |
| BC |
| BA1 |
| BC1 |
∴∠ABA1=∠CBC1,
∴△ABA1∽△CBC1,
∴
| S△ABA1 |
| S△CBC1 |
| AB |
| BC |
| 4 |
| 5 |
| 16 |
| 25 |
∵S△ABA1=4,
∴S△CBC1=
| 25 |
| 4 |
点评:本题考查了旋转的性质,等腰三角形的性质,相似三角形的判定与性质,难度适中,(2)中证明△ABA1∽△CBC1,是解题的关键.

练习册系列答案
相关题目
 (2013•河南模拟)如图,直线a∥直线b,∠1=∠2,∠3=150°,∠4的大小( )
(2013•河南模拟)如图,直线a∥直线b,∠1=∠2,∠3=150°,∠4的大小( ) (2013•河南模拟)如图,在平面直角坐标系中,Rt△OAB的三个顶点坐标分别是O(0,0),A(-1,2),B(-1,0)将△OAB先向左平移1个单位长度得到△O′A′B′,再将△O′A′B′绕点O′按顺时针方向旋转90°得到△O′A″B″,则点A″的坐标是( )
(2013•河南模拟)如图,在平面直角坐标系中,Rt△OAB的三个顶点坐标分别是O(0,0),A(-1,2),B(-1,0)将△OAB先向左平移1个单位长度得到△O′A′B′,再将△O′A′B′绕点O′按顺时针方向旋转90°得到△O′A″B″,则点A″的坐标是( )