Question

．（6分）如图，将腰长为的等腰Rt△ABC(∠C是直角)放在平面直角坐标系中的第二象限，其中点A在y轴上，点B在抛物线y＝ax²＋ax－2上，点C的坐标为(－1，0)．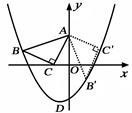

【小题1】(1)点A的坐标为        ，点B的坐标为        ；
【小题2】(2)抛物线的关系式为                      ，其顶点坐标为            ；
【小题3】(3)将三角板ABC绕顶点A逆时针方向旋转90°，到达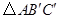的位置．请判断点、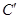是否在(2)中的抛物线上，并说明理由．

Answer 1

【小题1】(1)A(0，2)，B(，1)
【小题2】(2)解析式为；
顶点为()．
【小题3】(3)如图，过点作轴于点M，过点B作轴于点N，过点作
 轴于点P．
在Rt△AB′M与Rt△BAN中，
∵AB=AB′，∠AB′M=∠BAN=90°-∠B′AM，
∴ Rt△AB′M≌Rt△BAN．
∴B′M=AN=1，AM=BN=3，∴B′(1，)．
同理△AC′P≌△CAO，C′P=OA=2，AP=OC=1，
可得点C′(2，1)；
将点B′、C′的坐标代入，
可知点B′、C′在抛物线上．      解析:
略