题目内容
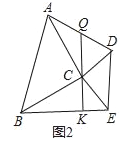
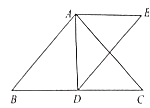
【题目】如图,在![]() 中,
中,![]() ,
,![]() 是中线,作
是中线,作![]() 关于
关于![]() 的轴对称图形
的轴对称图形![]() .
.
(1)直接写出![]() 和
和![]() 的位置关系;
的位置关系;
(2)连接![]() ,写出
,写出![]() 和
和![]() 的数量关系,并说明理由;
的数量关系,并说明理由;
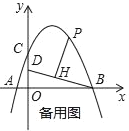
(3)当![]() ,
,![]() 时,在
时,在![]() 上找一点
上找一点![]() ,使得点
,使得点![]() 到点
到点![]() 与到点
与到点![]() 的距离之和最下小,求
的距离之和最下小,求![]() 的面积.
的面积.
【答案】(1)垂直;(2)![]() .理由见解析;(3)
.理由见解析;(3)![]() .
.
【解析】
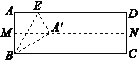
(1)根据对称点连线垂直于对称轴,即可确定AC⊥DE;(2)连接CE,证明四边形AECD是正方形,在结合三角形ABC是等腰三角形,即可说明;(3)先证明.△ACD≌△ABD,得到点B和点C关于AD成轴对称;连接![]() ,交
,交![]() 于点
于点![]() ,且当
,且当![]() ,
,![]() ,
,![]() 三点在同一条直线上,点
三点在同一条直线上,点![]() 到点
到点![]() 与到点
与到点![]() 的距离之和最小,然后结合(1)的结论,运用三角形的面积公式即可求得.
的距离之和最小,然后结合(1)的结论,运用三角形的面积公式即可求得.
解:(1)垂直
(2)![]() .理由如下:
.理由如下:
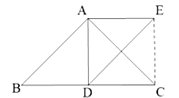
![]() 关于
关于![]() 的轴对称图形为
的轴对称图形为![]() .
.
![]() ,
,![]()
在![]() 和
和![]() 中,
中,
![]()
![]()
又![]() 是边
是边![]() 上的中线
上的中线
![]() .
.
![]() .
.
(3)在![]() 和
和![]() 中
中
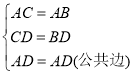
![]()
![]()
![]()
![]()
![]() 点
点![]() 和点
和点![]() 关于
关于![]() 成轴对称
成轴对称
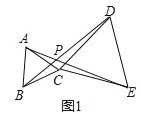
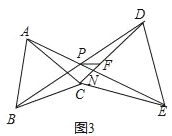
连接![]() ,交
,交![]() 于点
于点![]() ,如图所示
,如图所示
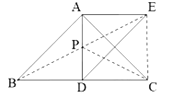
![]()
![]()
且当![]() ,
,![]() ,
,![]() 三点在同一条直线上,点
三点在同一条直线上,点![]() 到点
到点![]() 与到点
与到点![]() 的距离之和最小
的距离之和最小
![]()
![]()
在![]() 中,.
中,.![]()
由(1)知,![]() ,
,
![]()
![]()
![]()
![]()
![]()

练习册系列答案
相关题目