题目内容
如图，点C是AB上一点，O是圆心，且∠AOB=120°，则∠ACB= 度．
【答案】分析：设点E是优弧AB上的一点，则∠AEB=60°，由圆内接四边形的对角互补知，即可求∠ACB=180°-∠AEB=120°．
解答：
解：设点E是优弧AB上的一点，
∵∠AOB=120°，
∴∠AEB=60°，
∴∠ACB=180°-∠AEB=120°．
点评：本题利用了圆周角定理：在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半．和圆内接四边形的性质求解．
解答：
解：设点E是优弧AB上的一点，∵∠AOB=120°，
∴∠AEB=60°，
∴∠ACB=180°-∠AEB=120°．
点评：本题利用了圆周角定理：在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半．和圆内接四边形的性质求解．
练习册系列答案
相关题目
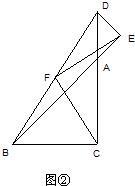
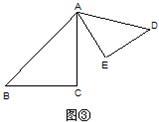
如图，点O是AB上的一点，OC为任意一条射线，另有OD，OE分别平分∠AOC，∠BOC．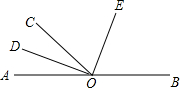
如图，点O是AB上的一点，OC为任意一条射线，另有OD，OE分别平分∠AOC，∠BOC．