题目内容
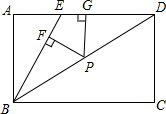 如图,已知,E是矩形ABCD边AD上一点,且BE=ED,P是对角线BD上任一点,PF⊥BE,PG⊥AD,垂足分别为F、G,你知道PF+PG与AB有什么关系吗?并证明你的结论.
如图,已知,E是矩形ABCD边AD上一点,且BE=ED,P是对角线BD上任一点,PF⊥BE,PG⊥AD,垂足分别为F、G,你知道PF+PG与AB有什么关系吗?并证明你的结论.
分析:在本题中,PF、PG和AB在表面上并没有关系,但是在连接PE后,由于把三角形BED分成了两个三角形,从而利用面积之间的等量关系,找出PF+PE和AB间的关系,看重转化思想.
解答: 解:PF+PG=AB.理由如下:
解:PF+PG=AB.理由如下:
连接PE,
则S△BEP+S△DEP=S△BED
即
BE•PF+
DE•PG=
DE•AB.
又∵BE=DE,
∴
DE•PF+
DE•PG=
DE•AB.
即
DE(PF+PG)=
DE•AB,
∴PF+PG=AB.
 解:PF+PG=AB.理由如下:
解:PF+PG=AB.理由如下:连接PE,
则S△BEP+S△DEP=S△BED
即
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
又∵BE=DE,
∴
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
即
| 1 |
| 2 |
| 1 |
| 2 |
∴PF+PG=AB.
点评:本题主要是考查矩形的基本性质及空间想象能力,有一定的思维容量.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
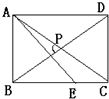 17、如图,已知四边形ABCD是矩形,对角线AC、BD相交于点P,∠APB=60°,点E在BC边上,且BE=BP,
17、如图,已知四边形ABCD是矩形,对角线AC、BD相交于点P,∠APB=60°,点E在BC边上,且BE=BP,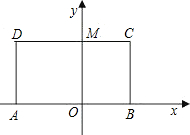 如图,已知四边形ABCD是矩形,且MO=MD=4,MC=3.
如图,已知四边形ABCD是矩形,且MO=MD=4,MC=3. (2013•湖州)如图,已知四边形ABCD是矩形,把矩形沿直线AC折叠,点B落在点E处,连接DE.若DE:AC=3:5,则
(2013•湖州)如图,已知四边形ABCD是矩形,把矩形沿直线AC折叠,点B落在点E处,连接DE.若DE:AC=3:5,则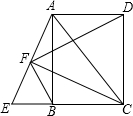 如图,已知点E是矩形ABCD的边CB延长线上一点,且CE=CA,连接AE,过点C作CF⊥AE,垂足为点F,连接BF、FD.
如图,已知点E是矩形ABCD的边CB延长线上一点,且CE=CA,连接AE,过点C作CF⊥AE,垂足为点F,连接BF、FD.