题目内容
如图,四边形ABCD、BEFG均为正方形.
(1)如图1,连接AG、CE,判断AG和CE的数量关系和位置关系并证明.
(2)将正方形BEFG绕点B顺时针旋转β角(0°<β<180°),如图2,连接AG、CE相交于点M,连接MB,求出∠EMB的度数.
(3)若BE=2,BC=6,连接DG,将正方形BEFG绕点B顺时针旋转β角(0°<β<180°),则在这个旋转过程中线段DG长度的取值范围 (直接填空,不写过程).
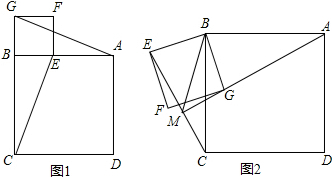
(1)如图1,连接AG、CE,判断AG和CE的数量关系和位置关系并证明.
(2)将正方形BEFG绕点B顺时针旋转β角(0°<β<180°),如图2,连接AG、CE相交于点M,连接MB,求出∠EMB的度数.
(3)若BE=2,BC=6,连接DG,将正方形BEFG绕点B顺时针旋转β角(0°<β<180°),则在这个旋转过程中线段DG长度的取值范围

考点:全等三角形的判定与性质,正方形的性质,旋转的性质
专题:
分析:(1)由条件证明Rt△GBA≌Rt△EBC可得出AG=CE,且∠GAB=∠BCE,可判定出其位置关系;
(2)过B作BP⊥EC,BQ⊥MA,垂足分别为P、Q,证明△BPE≌△BQG可得BP=BQ,而可知PM=BQ,所以可得出△BPM为等腰直角三角形,可求出∠EMB的度数;
(3)当点G在线段BD上时最短,当在初始位置时,DG最大,利用勾股定理可求得其长度,但旋转不到180°,可得出其范围.
(2)过B作BP⊥EC,BQ⊥MA,垂足分别为P、Q,证明△BPE≌△BQG可得BP=BQ,而可知PM=BQ,所以可得出△BPM为等腰直角三角形,可求出∠EMB的度数;
(3)当点G在线段BD上时最短,当在初始位置时,DG最大,利用勾股定理可求得其长度,但旋转不到180°,可得出其范围.
解答:解:(1)AG=CE,AG⊥CE,证明如下:
∵四边形ABCD、BEFG均为正方形,
∴∠GBA=∠EBC=90°,BG=BE,BA=BC,
在△GBA和△EBC中,
,
∴△GBA≌△EBC(SAS),
∴AG=CE,∠GAB=∠BCE,
∴∠BGA+∠BCE=∠BGA+∠GAB=90°,
∴AG⊥CE;
(2)如图,过B作BP⊥EC,BQ⊥MA,垂足分别为P、Q,
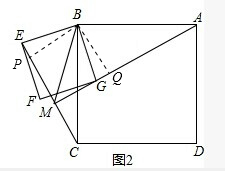
可知四边形BPMQ为矩形,
∴∠PBE+∠PBG=∠QBG+∠PBG=90°,
∴∠PBE=∠QBG,
在△BPE和△BQG中,
,
∴△BPE≌△BQG(AAS),
∴BP=BQ,且BQ=PM,
∴BP=PM,
∴△BPM为等腰直角三角形,
∴∠PMB=45°;
(3)当在初始位置时,DG最大,此时GC=6+2=8,CD=6,由勾股定理可求得DG=10,
当G点在线段BD上时,DG最小,此时BG=2,BD=6
,所以DG=6
-2,而旋转角取不到180°,
所以DG的范围为:6
-2≤DG<10,
故答案为:6
-2≤DG<10.
∵四边形ABCD、BEFG均为正方形,
∴∠GBA=∠EBC=90°,BG=BE,BA=BC,
在△GBA和△EBC中,
|
∴△GBA≌△EBC(SAS),
∴AG=CE,∠GAB=∠BCE,
∴∠BGA+∠BCE=∠BGA+∠GAB=90°,
∴AG⊥CE;
(2)如图,过B作BP⊥EC,BQ⊥MA,垂足分别为P、Q,

可知四边形BPMQ为矩形,
∴∠PBE+∠PBG=∠QBG+∠PBG=90°,
∴∠PBE=∠QBG,
在△BPE和△BQG中,
|
∴△BPE≌△BQG(AAS),
∴BP=BQ,且BQ=PM,
∴BP=PM,
∴△BPM为等腰直角三角形,
∴∠PMB=45°;
(3)当在初始位置时,DG最大,此时GC=6+2=8,CD=6,由勾股定理可求得DG=10,
当G点在线段BD上时,DG最小,此时BG=2,BD=6
| 2 |
| 2 |
所以DG的范围为:6
| 2 |
故答案为:6
| 2 |
点评:本题主要考查全等三角形的判定和性质及正方形的性质的应用,(2)中构造三角形全等、(3)中确定出最大值和最小值的位置是解题的关键.

练习册系列答案
相关题目
 如图是某地2014年黄瓜的销售价格y(元)随月份x变化的图象,请回答下列问题:
如图是某地2014年黄瓜的销售价格y(元)随月份x变化的图象,请回答下列问题: