题目内容
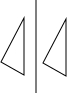
如图,矩形纸片ABCD中,AD=9cm,AB=3cm,将纸片沿虚线EF折叠,使得点D与点B重合,那么折痕EF的长度为______cm.


设BD于EF交于点O,则O是BD的中点.
在直角△ABD中,BD=
=
=3
cm;
则OD=
.
∵B、D关于EF对称,
∴∠EOD=90°,
又∵矩形ABCD中,∠A=90°,
∴∠A=∠EOD=90°.
在△ABD于△OED中,∠A=∠EOD=90°,∠ADB=∠ODE,
∴△ABD∽△OED.
∴
=
,
∴OE=
•AB=
×3=
cm.
∴EF=2OE=
cm.

在直角△ABD中,BD=
| AB2+AD2 |
| 81+9 |
| 10 |
则OD=
3
| ||
| 2 |
∵B、D关于EF对称,
∴∠EOD=90°,
又∵矩形ABCD中,∠A=90°,
∴∠A=∠EOD=90°.
在△ABD于△OED中,∠A=∠EOD=90°,∠ADB=∠ODE,
∴△ABD∽△OED.
∴
| OE |
| AB |
| OD |
| AD |
∴OE=
| OD |
| AD |
| ||||
| 9 |
| ||
| 2 |
∴EF=2OE=
| 10 |


练习册系列答案
相关题目