题目内容
 如图,CD为等腰直角△ABC斜边AB上的高,点E,F在直线BC上,∠EDF=45°,ED的延长线交CA的延长线于点G,连接FG.
如图,CD为等腰直角△ABC斜边AB上的高,点E,F在直线BC上,∠EDF=45°,ED的延长线交CA的延长线于点G,连接FG.(1)求证:
| DE |
| EF |
| AG |
| DG |
(2)若tan∠BFG=
| 3 |
| 4 |
分析:(1)根据条件可以求出∠CAB=∠CBA=45°,∠GAD=∠FBD=135°就可以证明△DEB∽△FED和△ADG∽△BDF,由相似三角形的性质就可以求出结论;
(2)在Rt△CGF中,tan∠CFG=
=
,设CG=3k,CF=4k,由勾股定理求出GF=5k,由条件及等腰直角三角形的性质可以求得∠CDG=∠FDG.作EH⊥FG于点H,由角平分线的性质就可以求出EC=EH.再根据三角函数值就可以用k表示出CE、EF.过点D作DM⊥CE于M,可以得出△DME∽△GCE,由其性质就可以得出DM=k,根据S△EDF=5建立方程求出k的值就可以求出结论.
(2)在Rt△CGF中,tan∠CFG=
| CG |
| CF |
| 3 |
| 4 |
解答:解:(1)∵CA=CB,
∴∠CAB=∠CBA.
∵∠CAB+∠CBA+∠ACB=180°,且∠ACB=90°,
∴∠CAB=∠CBA=45°.
∵∠EDF=45°,
∴∠EDF=∠EDB.
∵∠DEB=∠FED,
∴△DEB∽△FED,
∴
=
.
∵∠GDF=180°-∠EDF=135°,
∴∠ADG+∠BDF=180°-135°=45°.
∵∠CAB=∠CBA=45°,
∴∠GAD=∠FBD=135°,
∴∠ADG+∠AGD=180°-135°=45°.
∴∠BDF=∠ADG.
∵∠GAD=∠FBD=135°,
∴△AGD∽△BDF,
∴
=
,
∴
=
,
∴
=
.
(2)在Rt△CGF中,tan∠CFG=
=
,设CG=3k,CF=4k,由勾股定理,得
GF=5k.
∵△AGD∽△BDF,
∴
=
.
∵CD为等腰直角三角形ABC斜边上的高,
∴AD=BD=CD.
∴
=
,
∴
=
.
∵∠GAD=∠GDF=135°,
∴△AGD∽△DGF,
∴∠CDG=∠FDG.
∵∠GCE=90°,
∴EC⊥GC.
作EH⊥FG于点H,
∴EC=EH.(角平分线的性质)
在Rt△EHF中,tan∠EFH=
=
,
∴HF=
EH.
EF=
EH=
CE.
∵CE+EF=CF=4k,
∴CE=
k,EF=
k.
过点D作DM⊥CE于M.
∵CD为等腰直角△ABC斜边AB上的高,
∴∠DCB=45°,
∴∠CDM=45°,
∴∠DCB=∠CDM,
∴DM=CM.
∵∠GCB=∠DMB=90°,
∴DM∥CG.
∴△DME∽△GCE,
∴
=
,
∴
=
,
∴DM=k.
∵S△EDF=
EF.DM=
×
k•k=5,
解得:k=±2,
∵k=2不符合题意,舍去,
∴k=2,
∴GF=5k=10.
∴∠CAB=∠CBA.
∵∠CAB+∠CBA+∠ACB=180°,且∠ACB=90°,
∴∠CAB=∠CBA=45°.
∵∠EDF=45°,
∴∠EDF=∠EDB.
∵∠DEB=∠FED,
∴△DEB∽△FED,
∴
| DE |
| FE |
| DB |
| FD |
∵∠GDF=180°-∠EDF=135°,
∴∠ADG+∠BDF=180°-135°=45°.
∵∠CAB=∠CBA=45°,
∴∠GAD=∠FBD=135°,
∴∠ADG+∠AGD=180°-135°=45°.
∴∠BDF=∠ADG.
∵∠GAD=∠FBD=135°,
∴△AGD∽△BDF,
∴
| AG |
| BD |
| DG |
| DF |
∴
| AG |
| DG |
| BD |
| DF |
∴
| DE |
| EF |
| AG |
| DG |
(2)在Rt△CGF中,tan∠CFG=
| CG |
| CF |
| 3 |
| 4 |
GF=5k.
∵△AGD∽△BDF,
∴
| AG |
| BD |
| DG |
| DF |
∵CD为等腰直角三角形ABC斜边上的高,
∴AD=BD=CD.
∴
| AG |
| AD |
| DG |
| DF |
∴
| AG |
| DG |
| AD |
| DF |

∵∠GAD=∠GDF=135°,
∴△AGD∽△DGF,
∴∠CDG=∠FDG.
∵∠GCE=90°,
∴EC⊥GC.
作EH⊥FG于点H,
∴EC=EH.(角平分线的性质)
在Rt△EHF中,tan∠EFH=
| EH |
| FH |
| 3 |
| 4 |
∴HF=
| 4 |
| 3 |
EF=
| 5 |
| 3 |
| 5 |
| 3 |
∵CE+EF=CF=4k,
∴CE=
| 3 |
| 2 |
| 5 |
| 2 |
过点D作DM⊥CE于M.
∵CD为等腰直角△ABC斜边AB上的高,
∴∠DCB=45°,
∴∠CDM=45°,
∴∠DCB=∠CDM,
∴DM=CM.
∵∠GCB=∠DMB=90°,
∴DM∥CG.
∴△DME∽△GCE,
∴
| DM |
| CG |
| ME |
| CE |
∴
| DM |
| 3k |
| ||
|
∴DM=k.
∵S△EDF=
| 1 |
| 2 |
| 1 |
| 2 |
| 5 |
| 2 |
解得:k=±2,
∵k=2不符合题意,舍去,
∴k=2,
∴GF=5k=10.
点评:本题是一道综合性极强的试题,考查了勾股定理的运用,等腰直角三角形的性质的运用,相似三角形的判定及性质的运用,平行线的判定及性质的运用,一元二次方程的解法的运用,三角函数值的运用,解答时合理利用相似三角形的性质是关键.

练习册系列答案
 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案
相关题目
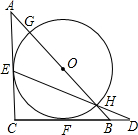 如图,△ABC是等腰直角三角形,AC=BC=a,以斜边AB上的点O为圆心的圆分别与AC、BC相切于点E、F,与AB分别相交于点G、H,且EH的延长线与CB的延长线交于点D,则CD的长为( )
如图,△ABC是等腰直角三角形,AC=BC=a,以斜边AB上的点O为圆心的圆分别与AC、BC相切于点E、F,与AB分别相交于点G、H,且EH的延长线与CB的延长线交于点D,则CD的长为( )A、
| ||||
B、
| ||||
C、
| ||||
D、(
|
 1、如图,△ABC是等腰直角三角形,∠A=90°,CD∥BE,∠1+∠2=83°,则∠2的度数为( )
1、如图,△ABC是等腰直角三角形,∠A=90°,CD∥BE,∠1+∠2=83°,则∠2的度数为( ) 如图,△ABC是等腰直角三角形,AC=BC=2,以斜边AB上的点O为圆心的圆分别与AC、BC相切于点E、F,与AB分别相交于点G、H,且EH的延长线与CB的延长线交于点D,则CD的长为
如图,△ABC是等腰直角三角形,AC=BC=2,以斜边AB上的点O为圆心的圆分别与AC、BC相切于点E、F,与AB分别相交于点G、H,且EH的延长线与CB的延长线交于点D,则CD的长为 如图,△ACB为等腰直角三角形,点D为斜边AB上一点,连CD,DE⊥CD,DE=CD.连AE.求证:AE∥BC.
如图,△ACB为等腰直角三角形,点D为斜边AB上一点,连CD,DE⊥CD,DE=CD.连AE.求证:AE∥BC.