题目内容
如图,在Rt△ABC中,∠ACB=90°,AC=6㎝,BC=8㎝,P为BC的中点.动点Q从点P出发,沿射线PC方向以2㎝/s的速度运动,以P为圆心,PQ长为半径作圆.设点Q运动的时间为t s.
⑴当t=1.2时,判断直线AB与⊙P的位置关系,并说明理由;
⑵已知⊙O为△ABC的外接圆,若⊙P与⊙O相切,求t的值.
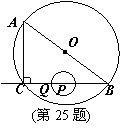

解:⑴ ————5分
直线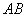 与⊙P相切.
与⊙P相切.
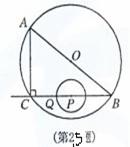
如图,过点P作PD⊥AB, 垂足为D.
在Rt△ABC中,∠ACB=90°,∵AC=6cm,BC=8cm,
∴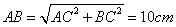 .∵P为BC的中点,∴PB=4cm.
.∵P为BC的中点,∴PB=4cm.
∵∠PDB=∠A CB=90°,∠PBD=∠ABC.∴△PBD∽△ABC.
CB=90°,∠PBD=∠ABC.∴△PBD∽△ABC.
∴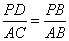 ,即
,即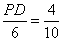 ,∴PD =2.4(cm) .
,∴PD =2.4(cm) .
当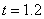 时,
时, (cm)
(cm)
∴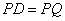 ,即圆心
,即圆心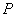 到直线
到直线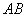 的距离等于⊙P的半径.
的距离等于⊙P的半径.
∴直线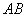 与⊙P相切.
与⊙P相切.
⑵ ————5分
∵∠ACB=90°,∴AB为△ABC的外切圆的直径.∴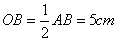 .
.
连接OP.∵P为BC的中点,∴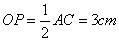 .
.
∵点P在⊙O内部,∴⊙P与⊙O只能内切.
∴ 或
或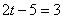 ,∴
,∴ =1或4.
=1或4.
∴⊙P与⊙O相切时,t的值为1或4.

练习册系列答案
相关题目
某风景区的门票价格如下表所示:
| 购票人数 | 1~50人 | 51~100人 | 100人以上 |
| 票价 | 100元/人 | 80元/人 | 50元/人 |
某校七年级甲、乙两班共100多人去该公园举行联欢活动,其中甲班50多人,乙班不足50人.如果以班为单位分别买票,两个班一共应付9200元;如果两个班联合起来作为一团体购票,一共只要付5150元.问:甲、乙两班分别有多少人?
下列四种图形既是中心对称图形又是轴对称图形的是( )
|
| A. | 等腰三角形 | B. | 等边三角形 | C. | 平行四边形 | D. | 矩形 |




 将函数y=Kx+K与函数y=的大致图象画在同一直角坐标系中,正确的函数图象是( )
将函数y=Kx+K与函数y=的大致图象画在同一直角坐标系中,正确的函数图象是( )


