题目内容
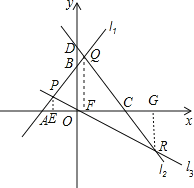
【题目】如图,已知直线l1:y=x+3与x轴交于点A,与y轴交于点B,与直线l2:y=﹣![]() x交于点P.直线l3:y=﹣
x交于点P.直线l3:y=﹣![]() x+4与x轴交于点C,与y轴交于点D,与直线l1交于点Q,与直线l2交于点R.
x+4与x轴交于点C,与y轴交于点D,与直线l1交于点Q,与直线l2交于点R.
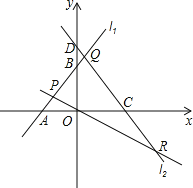
(1)点A的坐标是 ,点B的坐标是 ,点P的坐标是 ;
(2)将△POB沿y轴折叠后,点P的对应点为P′,试判断点P′是否在直线l3上,并说明理由;
(3)求△PQR的面积.
【答案】(1)(﹣3,0),(0,3),(﹣2,1);(2)见解析;(3)![]() .
.
【解析】
试题分析:(1)直线l1:y=x+3与x轴交于点A,与y轴交于点B,令y=0,求得x=﹣3,令x=0,求得y=3,得到A、B的坐标将直线l1:y=x+3和直线l2:y=﹣![]() x联立组成有关x、y的方程组,解方程就能求出两直线的交点P坐标;
x联立组成有关x、y的方程组,解方程就能求出两直线的交点P坐标;
(2)求得P′的坐标,代入y=﹣![]() x+4即可判断;
x+4即可判断;
(3)求得Q、R、C点的坐标,然后根据即可求得.
解:(1)∵直线l1:y=x+3与x轴交于点A,与y轴交于点B,
∴令y=0,求得x=﹣3,令x=0,求得y=3,
∴A(﹣3,0)、B(0,3),
∵直线l1与直线l2y=﹣![]() x交于点P.
x交于点P.
∴解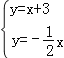 得
得![]() ,
,
∴P(﹣2,1),
故答案为:(﹣3,0),(0,3),(﹣2,1);
(2)点P在直线l3上
∵P(﹣2,1),且将△POB沿y轴折叠后,点P与点P关于y轴对称,
∴P(2,1),
当x=2时,代入y=﹣![]() x+4得y=﹣
x+4得y=﹣![]() ×2+4=1,
×2+4=1,
∴点P在直线l3上;
(3)分别过点P作PE⊥x轴于F,过点Q作QF⊥x轴于F,过点R作RG⊥x轴于G,
由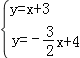 得
得![]() ,
,
∴Q(![]() ,
,![]() ),
),
由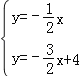 得
得![]()
∴R(4,﹣2),
对于y=﹣![]() x+4,则y=0得x=
x+4,则y=0得x=![]() ,
,
∴C(![]() ,0),
,0),
∴S△AQC=![]() AC×QF=
AC×QF=![]() ×(
×(![]() +3)×
+3)×![]() =
=![]() ,S△OCR=
,S△OCR=![]() OCGR=
OCGR=![]() ×
×![]() ×2=
×2=![]() ,S△AOP=
,S△AOP=![]() OAPE=
OAPE=![]() ×3×1=
×3×1=![]() ,
,
∴S△PQR=S△AQC+S△OCR﹣S△AOP=![]() +
+![]() ﹣
﹣![]() =
=![]() .
.

【题目】某食品公司产销一种食品,已知每月的生产成本y1与产量x之间是一次函数关系,函数y1与自变量z(kg)的部分对应值如下表:
x(单位:kg) | 10 | 20 | 30 |
y1(单位:/元) | 3030 | 3060 | 3090 |
(1)求y1与x之间的函数关系式;
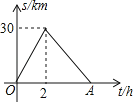
(2)经过试销发现,这种食品每月的销售收入y2(元)与销量x(kg)之间满足如图所示的函数关系
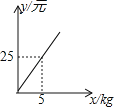
①y2与x之间的函数关系式为 ;
②假设该公司每月生产的该种食品均能全部售出,那么该公司每月至少要生产该种食品多少kg,才不会亏损?