题目内容
已知:在△ABC中,AC=BC,∠ACB=90°,点D是AB的中点,点E是AB边上一点.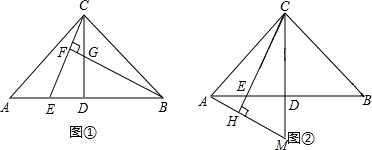
(1)直线BF垂直于CE于点F,交CD于点G(如图1),求证:AE=CG;
(2)直线AH垂直于CE,垂足为H,交CD的延长线于点M(如图2),求证:△BCE≌△CAM.
【考点】全等三角形的判定与性质;等腰直角三角形.
【分析】(1)先证出∠ACE=∠CBG,再由ASA证明△ACE≌△CBG,得出对应边相等即可;
(2)先证出∠CEB=∠CMA,再由AAS证明△BCE≌△ACM.
【解答】解:(1)∵点D是AB的中点,AC=BC,∠ACB=90°,
∴CD⊥AB,∠ACD=∠BCD=45°,∠CAD=∠CBD=45°.
∴∠CAE=∠BCG.
又BF⊥CE,
∴∠CBG+∠BCF=90°.
又∠ACE+∠BCF=90°,
∴∠ACE=∠CBG.
在△AEC和△CGB中,

∴△AEC≌△CGB.
∴AE=CG.
(2)∵CH⊥HM,CD⊥ED,
∴∠CMA+∠MCH=90°,∠BEC+∠MCH=90°.
∴∠CMA=∠BEC.
又AC=BC,∠ACM=∠CBE=45°,
在△BCE和△CAM中

∴∠BCE≌△CAM(AAS).
【点评】本题考查了全等三角形的判定与性质;熟练掌握全等三角形的判定方法是解决问题的关键.

练习册系列答案
相关题目

 |_____
|_____ _____﹣(﹣
_____﹣(﹣ );
); 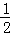 y2)],其中:x=﹣1,y=2.
y2)],其中:x=﹣1,y=2.