题目内容
如图，Rt△ABC中，AB=3，∠B=40°，则AC=（ ）| A、3cos50° | ||
| B、3tan40° | ||
| C、3sin50° | ||
D、
|
考点：锐角三角函数的定义
专题：
分析：根据正弦定义可得AC=3sin40°，再根据正弦与余弦的关系可得sin40°=cos50°，进而可得AC=3cos50°．
解答：解：∵sinB=
，
∴AC=AB•sinB，
∵AB=3，∠B=40°，
∴AC=3sin40°，
∵sin40°=cos50°，
∴AC=3cos50°，
故选：A．
| AC |
| AB |
∴AC=AB•sinB，
∵AB=3，∠B=40°，
∴AC=3sin40°，
∵sin40°=cos50°，
∴AC=3cos50°，
故选：A．
点评：此题主要考查了锐角三角函数定义，关键是掌握正弦：我们把锐角A的对边a与斜边c的比叫做∠A的正弦，记作sinA．
练习册系列答案
开心练习课课练与单元检测系列答案
相关题目
下列函数中，y随x的增大而增大的是（ ）
| A、y=-2x+3 | ||
B、y=-
| ||
C、y=
| ||
| D、y=-2x2（x＞0） |
如图所示，△ABC是边长为4厘米的等边三角形，两个动点P，Q同时从A点出发，点P以1厘米/秒的速度沿A→C→B的方向运动，点Q以2厘米/秒的速度沿A→B→C的方向运动，作CH⊥AB于H点，设P、Q运动的时间为t秒．（
）-1的计算结果为（ ）
| 1 |
| 2 |
A、
| ||
| B、-2 | ||
| C、2 | ||
D、-
|
如图，DE∥BC，则下列比例式错误的是（ ）A、
| ||||
B、
| ||||
C、
| ||||
D、
|
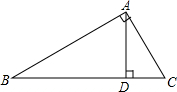如图，在Rt△ABC中，∠BAC=90°，AD⊥BC于点D，求证：AD2=CD•BD．
如图，AB⊥BD，∠DBE+∠E=90°，判断AB与CD是否平行，并说明理由．