题目内容
已知:在△ABC中,BC=2AC,∠DBC=∠ACB,BD=BC,CD交线段AB于点E.
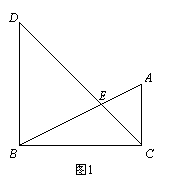
(1)如图l,当∠ACB=90°时,直接写出线段DE、CE之间的数量关系;
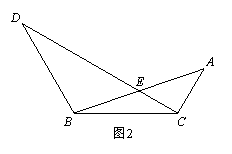
(2)如图2,当∠ACB=120°时,求证:DE=3CE;
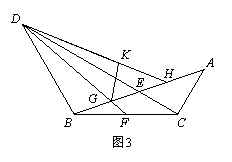
 (3)如图3,在(2)的条件下,点F是BC边的中点,连接DF,DF与AB交于G,△DKG和△DBG关于直线DG对称(点B的对称点是点K),
(3)如图3,在(2)的条件下,点F是BC边的中点,连接DF,DF与AB交于G,△DKG和△DBG关于直线DG对称(点B的对称点是点K),![]() 延长DK交AB于点H.若BH=10,求CE的长.
延长DK交AB于点H.若BH=10,求CE的长.
 |
(1)DE=2CE………………………1分
(2)证明:过点B作BM⊥DC于M
∵BD=BC,
∴DM=CM, ………………………..2分
∴∠DMB=∠CMB=90°,∠DBM=∠CBM=![]() ∠DBC=60°
∠DBC=60°
∴∠MCB=30° BM=![]() BC
BC
 ∵BC=2AC,
∵BC=2AC,
∴BM=AC.
∵∠ACB=120°,
∴∠ACE=90°.
∴∠BME=∠ACE
∵∠MEB=∠AEC
∴△EMB≌△ECA
∴ME=CE=![]() CM ………………………3分
CM ………………………3分
∴DE=3EC ………………………………4分
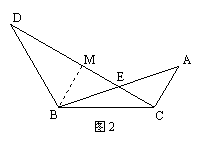
(3) 过点B作BM⊥DC于M,过点F作FN⊥DB交DB的延长线于点N.
∵∠DBF=120°, ∴∠FBN=60°. ∴FN=![]() BF,BN=
BF,BN=![]() BF ……5分
BF ……5分
∵DB=BC=2BF, DN=DB+BN=![]() BF
BF
 ∴DF=
∴DF=![]() BF
BF
∵AC=![]() BC,BF=
BC,BF=![]() BC
BC
∴AC=BF
∵∠DBC=∠ACB
∴△DBF≌BCA
∴∠BDF=∠CBA.
∵∠BFG=∠DFB,
∴△FBG∽△FDB
∴![]()
∴![]() ,∴
,∴![]() BF
BF
∴DG=![]() BF,BG=
BF,BG=![]() BF
BF
∵△DKG和△DBG关于直线DG对称,
∴∠GDH=∠BDF.∠ABC=∠GDH.
∵∠BGF=∠DGA,
∴△BGF∽△DGH.
∴![]() .
.
∴GH=![]() BF.
BF.
∵BH=BG+GH=![]() BF=10,
BF=10,
∴BF=![]() . …………………………….6分
. …………………………….6分
∴BC=2BF=4![]() ,CM=
,CM=![]()
∴CD=2CM=![]() .
.
∵DE=3EC
∴EC=![]() CD=
CD=![]() ……………………………..7分
……………………………..7分

 阅读快车系列答案
阅读快车系列答案 25、已知:在△ABC中AB=AC,点D在CB的延长线上.
25、已知:在△ABC中AB=AC,点D在CB的延长线上. (1)化简:(a-
(1)化简:(a- 20、如图,已知,在△ABC中,∠ABC和∠ACB的平分线交于点M,ME∥AB交BC于点E,MF∥AC交BC于点F.求证:△MEF的周长等于BC的长.
20、如图,已知,在△ABC中,∠ABC和∠ACB的平分线交于点M,ME∥AB交BC于点E,MF∥AC交BC于点F.求证:△MEF的周长等于BC的长. 12、已知,在△ABC中,AB=AC=x,BC=6,则腰长x的取值范围是
12、已知,在△ABC中,AB=AC=x,BC=6,则腰长x的取值范围是
 已知:在△ABC中,∠B<∠C,AD平分∠BAC,AE⊥BC,垂足为点E.∠B=38°,∠C=70°.
已知:在△ABC中,∠B<∠C,AD平分∠BAC,AE⊥BC,垂足为点E.∠B=38°,∠C=70°.