题目内容
如图,直线y=x,点A1坐标为(1,0),过点A1作x轴的垂线交直线于点B1,以原点O为圆心,OB1长为半径画弧交x轴于点A2,再过点A2作x轴的垂线交直线于点B2,以原点O为圆心,OB2长为半径画弧交x轴于点A3,…按此作法进行去,点Bn的坐标为 (n为正整数).
【答案】分析:由A1(1,0),可知B1的横坐标为1,由于B1,B2,B3,..,Bn都在直线y=x上,可知B1,B2,B3,..,Bn各点的横坐标与纵坐标相等,即B1(1,1),由勾股定理得OB1= ,由此可得A2(
,由此可得A2( ,0),则B2(
,0),则B2( ,
, ),由勾股定理得OB2=2,则A3(2,0),则B3(2,2),…,由此得出一般结论.
),由勾股定理得OB2=2,则A3(2,0),则B3(2,2),…,由此得出一般结论.
解答:解:∵B1,B2,B3,…,Bn都在直线y=x上,
∴B1,B2,B3,…,Bn各点的横坐标与纵坐标相等,
由A1(1,0),得B1(1,1),
此时OB1= ,
,
可知,A2( ,0),则B2(
,0),则B2( ,
, ),
),
同理可得B3(2,2),…,
则Bn( ,
, ).
).
故答案为:( ,
, ).
).
点评:本题考查了一次函数的综合运用.关键是明确直线y=x上点的横坐标与纵坐标相等特点,由易到难,由特殊到一般,得出规律.
 ,由此可得A2(
,由此可得A2( ,0),则B2(
,0),则B2( ,
, ),由勾股定理得OB2=2,则A3(2,0),则B3(2,2),…,由此得出一般结论.
),由勾股定理得OB2=2,则A3(2,0),则B3(2,2),…,由此得出一般结论.解答:解:∵B1,B2,B3,…,Bn都在直线y=x上,
∴B1,B2,B3,…,Bn各点的横坐标与纵坐标相等,
由A1(1,0),得B1(1,1),
此时OB1=
 ,
,可知,A2(
 ,0),则B2(
,0),则B2( ,
, ),
),同理可得B3(2,2),…,
则Bn(
 ,
, ).
).故答案为:(
 ,
, ).
).点评:本题考查了一次函数的综合运用.关键是明确直线y=x上点的横坐标与纵坐标相等特点,由易到难,由特殊到一般,得出规律.

练习册系列答案
 单元期中期末卷系列答案
单元期中期末卷系列答案
相关题目
 14、如图,直线y=kx+b经过点A(-1,-2)和B(-2,0),直线y=2x过点A,则不等式2x<kx+b≤0的解集为
14、如图,直线y=kx+b经过点A(-1,-2)和B(-2,0),直线y=2x过点A,则不等式2x<kx+b≤0的解集为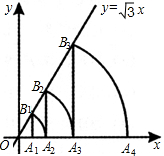 如图,直线
如图,直线 如图,直线AE∥BD,点C在BD上,若AE=5,BD=8,△ABD的面积为16,则△ACE的面积为
如图,直线AE∥BD,点C在BD上,若AE=5,BD=8,△ABD的面积为16,则△ACE的面积为 已知:如图,直线y=kx+b经过点A、B.
已知:如图,直线y=kx+b经过点A、B. 如图,直线AB⊥CD于点O,直线EF经过点O,∠1=35°.求∠2、∠3及∠EOB的度数.
如图,直线AB⊥CD于点O,直线EF经过点O,∠1=35°.求∠2、∠3及∠EOB的度数.