Question

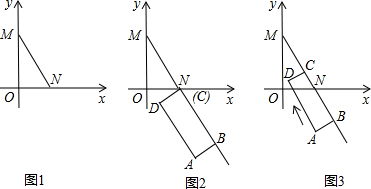
如图1，将斜边长为6cm的直角三角板放置在直角坐标系中，直角顶点与原点重合，直角边分别与x轴、y轴重合，且∠MNO=60°．将长和宽分别为6cm、2cm的直尺ABCD的长边与直线MN重合，其中C点与N点重合（如图2）．三角板固定不动，直尺以1cm/s的速度沿着直线MN向左上方滑动（如图3），直到C点与M点重合为止．设移动ts后，直尺和三角板重叠部分的面积为Scm²．
求：（1）直线MN的函数关系式；
（2）S与t之间的函数关系式，并求S的最大值．

Answer 1

分析：（1）由题意斜边长为6cm的直角三角板且∠MNO=60°，可以很容易求出M、N的坐标，根据两点的坐标求出函数式．
（2）随着直尺的移动会出现三种情况，分类讨论：①重叠部分为30度角的直角三角形．②重叠部分为直角梯形．③重叠部分为五边形．比较3种情况的最大值．

解答：解：（1）∵直角三角形的斜边为6cm∠MND=60°
∴OM=3

3

cm  ON=3cm
∴M点坐标为（0，3

3

）  N点坐标为（3，0）
∴直线MN的函数关系式为y=-

3

x+3

3

（2）
①重叠部分为30度角的直角三角形时：
S=

1

2

×t×

3

t=

3

2

t2
当D点到x轴时不再是30度角的直角三角形，
此时t=

2 3

3

s
∴S=

3

2

t2（0≤t≤

2 3

3

）
②重叠部分为直角梯形时：S=

1

2

×(t-

2 3

3

+t)×2=2t-

2 3

3

点D到Y轴时不再是直角梯形，此时t=6-2

3

s
∴S=2t-

2 3

3

（

2 3

3

＜t≤6-2

3

）
③重叠部分为五边形时：S=

1

2

×3×3

3

-

1

2

×(6-t)×(6-t)×

3

3

-

1

2

×(3-

4 3

3

)×(3-

4 3

3

)×

3

S=-

3

6

×(6-t)2+12-

24 3

9

C点与M点重合时，t=6
∴S=-

3

6

×(6-t)2+12-

24 3

9

（6-2

3

＜t≤6）
综上所述，根据图形可以看出面积总是在增大，即当t=6时面积最大，为12-

8 3

3

．

点评：本题主要考查一次函数的应用，题中要注意不同情况的不同函数以及其定义域．在图形中渗透运动的观点是中考中经常出现的问题，在平时的训练中要注意这方面的培养．