题目内容
如图,抛物线y=![]() x2+mx+n交x轴于A、B两点,交y轴于点C,点P是它的顶点,点A的横坐标是-3,点B的横坐标是1.
x2+mx+n交x轴于A、B两点,交y轴于点C,点P是它的顶点,点A的横坐标是-3,点B的横坐标是1.

(1)求m、n的值;
(2)求直线PC的解析式;
(3)请探究以点A为圆心、直径为5的圆与直线PC的位置关系,并说明理由.(参考数据:![]() ≈1.41,
≈1.41,![]() ≈1.73,
≈1.73,![]() ≈2.24)
≈2.24)
(1)140;2800;10;1500(2)z=120n+300(10<n≤30)(3)
【解析】解:(1)140;2800;10;1500。
(2)当10<n≤30时,设z=kn+b(k≠0),
∵函数图象经过点(10,1500),(30,3900),
∴![]() ,解得
,解得![]() 。
。
∴当10<n≤30时, z与n之间的函数关系式为z=120n+300(10<n≤30)。
(3)当10<m≤30时,设y=k1m+b1,
∵函数图象经过点(10,160),(30,120),![]()
∴![]() ,解得
,解得![]() 。
。
∴![]() 。
。
∵m+n=30,∴n=30-m。
∴①当10<m≤20时,10<n≤20,
![]() 。
。
②当20<m≤30时,0<n≤10,
![]() 。
。
∴w与m之间的函数关系式为 。
。
(1)根据图象数据解答即可:
由图可知,如果种植蔬菜20亩,则小张种植每亩蔬菜的工资是(160+120)=140元,小张应得的工资总额是:140×20=2800元。此时,小李种植水果:30﹣20=10亩,小李应得的报酬是1500元。
(2)设z=kn+b(k≠0),然后利用待定系数法求一次函数解析式即可。
(3)先求出20<m≤30时y与m的函数关系式,再分①10<m≤20时,10<m≤20;②20<m≤30时,0<n≤10两种情况,根据总费用等于两人的费用之和列式整理即可得解。

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案
相关题目
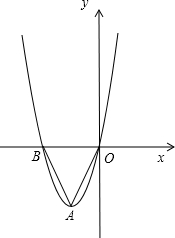 如图,抛物线y=x2+4x与x轴分别相交于点B、O,它的顶点为A,连接AB,AO.
如图,抛物线y=x2+4x与x轴分别相交于点B、O,它的顶点为A,连接AB,AO. 16、如图,抛物线y=-x2+2x+m(m<0)与x轴相交于点A(x1,0)、B(x2,0),点A在点B的左侧.当x=x2-2时,y
16、如图,抛物线y=-x2+2x+m(m<0)与x轴相交于点A(x1,0)、B(x2,0),点A在点B的左侧.当x=x2-2时,y 已知如图,抛物线y=x2+(k2+1)x+k+1的对称轴是直线x=-1,且顶点在x轴上方.设M是直线x=-1左侧抛物线上的一动点,过点M作x轴的垂线MG,垂足为G,过点M作直线x=-1的垂线MN,垂足为N,直线x=-1与x轴的交于H点,若M点的横坐标为x,矩形MNHG的周长为l.
已知如图,抛物线y=x2+(k2+1)x+k+1的对称轴是直线x=-1,且顶点在x轴上方.设M是直线x=-1左侧抛物线上的一动点,过点M作x轴的垂线MG,垂足为G,过点M作直线x=-1的垂线MN,垂足为N,直线x=-1与x轴的交于H点,若M点的横坐标为x,矩形MNHG的周长为l. (2013•扬州)如图,抛物线y=x2-2x-8交y轴于点A,交x轴正半轴于点B.
(2013•扬州)如图,抛物线y=x2-2x-8交y轴于点A,交x轴正半轴于点B.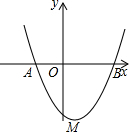 如图,抛物线y=x2-2x-3与x轴分别交于A,B两点.
如图,抛物线y=x2-2x-3与x轴分别交于A,B两点.