题目内容
.如图(1),在直角△ABC中, ∠ACB=90![]() ,CD⊥AB,垂足为D,点E在AC上,BE交CD于点G,EF⊥BE交AB于点F,若AC=mBC,CE=nEA(m,n为实数).
,CD⊥AB,垂足为D,点E在AC上,BE交CD于点G,EF⊥BE交AB于点F,若AC=mBC,CE=nEA(m,n为实数).
试探究线段EF与EG的数量关系.
(1) 如图(2),当m=1,n=1时,EF与EG的数量关系是
证明:
(2) 如图(3),当m=1,n为任意实数时,EF与EG的数量关系是
证明
(3) 如图(1),当m,n均为任意实数时,EF与EG的数量关系是
(写出关系式,不必证明)
(1)图甲:连接DE,
∵AC=mBC,CD⊥AB,当m=1,n=1时
∴AD=BD,∠ACD=45°,
 ∴CD=AD=
∴CD=AD= AB,
AB,
∵AE=nEC,
∴DE=AE=EC=![]() AC,
AC,
∴∠EDC=45°,DE⊥AC,
∵∠A=45°,
∴∠A=∠EDG,
∵EF⊥BE,
∵∠AEF+∠FED=∠EFD+∠DEG=90°,
∴∠AEF=∠DEG,
∴△AEF≌△DEG(ASA),
∴EF=EG.
(2)解:EF=![]() EG证明:作EM⊥AB于点M,EN⊥CD于点N,
EG证明:作EM⊥AB于点M,EN⊥CD于点N,
∵EM∥CD,
 ∴△AEM∽△ACD,
∴△AEM∽△ACD,
∴![]()
即EM=![]() CD,
CD,
同理可得,EN=![]() AD,
AD,
∵∠ACB=90°,CD⊥AB,
∴tanA=![]() ,
,
∴![]() ,
,
又∵EM⊥AB,EN⊥CD,
∴∠EMF=∠ENG=90°,
∵EF⊥BE,
∴∠FEM=∠GEN,
∴△EFM∽△EGN,
∴![]() ,
,
即EF=![]() EG;
EG;
(3)EF=![]() EG.
EG.
解析:略

练习册系列答案
 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案
相关题目
 如图,矩形纸片ABCD在直角坐标系中如图所示,A(-9,1),B(-1,1)C(-1,7)将矩形纸片沿AC折叠,B点落在E处,AE交CD于点F,则F点坐标为( )
如图,矩形纸片ABCD在直角坐标系中如图所示,A(-9,1),B(-1,1)C(-1,7)将矩形纸片沿AC折叠,B点落在E处,AE交CD于点F,则F点坐标为( )A、(-
| ||
B、(-
| ||
C、(-
| ||
D、(
|
 如图,已知:在直角△ABC中,∠C=90°,BD平分∠ABC且交AC于D.
如图,已知:在直角△ABC中,∠C=90°,BD平分∠ABC且交AC于D.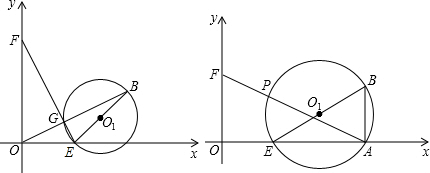
 如图,已知:在直角梯形ABCD中,AB∥CD,AD⊥CD,AB=BC,又AE⊥BC于E
如图,已知:在直角梯形ABCD中,AB∥CD,AD⊥CD,AB=BC,又AE⊥BC于E