题目内容
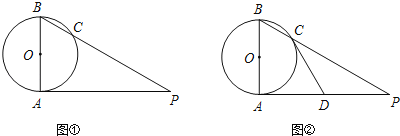
【题目】如图所示，图1、图2分别是
的网格，网格中的每个小正方形的边长均为1．请按下列要求分别画出相应的图形，且所画图形的每个顶点均在所给小正方形的顶点上．
(1)在图1中画出一个周长为
的菱形
(非正方形)；
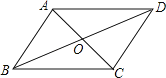
(2)在图2中画出一个面积为9的平行四边形
，且满足
，请直接写出平行四边形的周长．
【答案】（1）见解析；（2）见解析，周长为：
＋6．
【解析】
（1）利用数形结合的思想画出边长为
菱形即可．
（2）利用数形结合的思想解决问题即可．
解：（1）∵菱形
周长为
，
∴菱形的边长为，
如图1所示，菱形ABCD即为所求．
（2）如图2中，平行四边形MNPQ即为所求．
∵如图所示，∠MNP=45°，∠MPN=90°，
∴NP=MP，
又∵面积为9，
∴NPMP=9，
∴NP=MP=3，
∴MN=
，
∴周长为：＋6．
练习册系列答案
开心快乐假期作业暑假作业西安出版社系列答案
名题训练系列答案
相关题目
【题目】某工厂设计了一款成本为20元/件的工艺品投放市场进行试销，经过调查，得到如下数据：
销售单价x（元∕件） | … | 30 | 40 | 50 | 60 | … |
每天销售量y（件） | … | 500 | 400 | 300 | 200 | … |
（1）研究发现，每天销售量y与单价x满足一次函数关系，求出y与x的关系式；
（2）当地物价部门规定，该工艺品销售单价最高不能超过45元/件，那么销售单价定为多少时，工艺厂试销该工艺品每天获得的利润8000元？
