题目内容
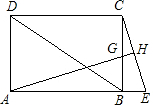 如图:BD是矩形ABCD的对角线,E是AB延长线上的一点,且AE=BD,过A作AH⊥CE于H,交BC于G.
如图:BD是矩形ABCD的对角线,E是AB延长线上的一点,且AE=BD,过A作AH⊥CE于H,交BC于G.(1)求证:H为CE的中点;
(2)若HG•HA=10,AD:AB=3:4,求AD与AB的长.
分析:(1)先连接AC,由于四边形ABCD是矩形,于是AC=BD,而AE=BD,那么AC=AE,而AH⊥BC,利用等腰三角形三线合一定理可证H是BC的中点;
(2)先设AB=4x,AD=3x,由于∠E+∠BCE=90°,∠ACE+∠CAH=90°,∠E=∠ACE,易求∠GCH=∠CAH,而∠AHC=∠CHG=90°,从而可证△AHC∽△CHG,利用比例线段可求CH,进而可求BC,易知BE=x,在Rt△CBE中,有(3x)2+x2=(2
)2,可求x,从而易求AB、AD.
(2)先设AB=4x,AD=3x,由于∠E+∠BCE=90°,∠ACE+∠CAH=90°,∠E=∠ACE,易求∠GCH=∠CAH,而∠AHC=∠CHG=90°,从而可证△AHC∽△CHG,利用比例线段可求CH,进而可求BC,易知BE=x,在Rt△CBE中,有(3x)2+x2=(2
| 10 |
解答: (1)证明:如右图所示,连接AC,
(1)证明:如右图所示,连接AC,
∵四边形ABCD是矩形,
∴AC=BD,
又∵AE=BD,
∴AC=AE,
∵AH⊥BC,
∴H是CE的中点;
(2)解:如右图所示,连接AC,
设AD=3x,AB=4x,
∵∠E+∠BCE=90°,∠ACE+∠CAH=90°,∠E=∠ACE,
∴∠GCH=∠CAH,
又∵∠AHC=∠CHG=90°,
∴△AHC∽△CHG,
∴
=
,
∴CH2=10,
∴EC=2
,
∵AC=AE,
∴BE=4x-3x=x,
在Rt△CBE中,有(3x)2+x2=(2
)2,
解得x=2,
∴AB=8,AD=6.
 (1)证明:如右图所示,连接AC,
(1)证明:如右图所示,连接AC,∵四边形ABCD是矩形,
∴AC=BD,
又∵AE=BD,
∴AC=AE,
∵AH⊥BC,
∴H是CE的中点;
(2)解:如右图所示,连接AC,
设AD=3x,AB=4x,
∵∠E+∠BCE=90°,∠ACE+∠CAH=90°,∠E=∠ACE,
∴∠GCH=∠CAH,
又∵∠AHC=∠CHG=90°,
∴△AHC∽△CHG,
∴
| CH |
| GH |
| AH |
| CH |
∴CH2=10,
∴EC=2
| 10 |
∵AC=AE,
∴BE=4x-3x=x,
在Rt△CBE中,有(3x)2+x2=(2
| 10 |
解得x=2,
∴AB=8,AD=6.
点评:本题考查了矩形的性质、等腰三角形三线合一定理、相似三角形的判定和性质、勾股定理.解题的关键是连接AC,并证明△AHC∽△CHG.

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案
相关题目
 称(要求:在原图中作图,不写作法,不证明,保留作图痕迹).
称(要求:在原图中作图,不写作法,不证明,保留作图痕迹).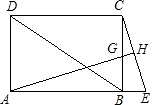 如图:BD是矩形ABCD的对角线,E是AB延长线上的一点,且AE=BD,过A作AH⊥CE于H,交BC于G.
如图:BD是矩形ABCD的对角线,E是AB延长线上的一点,且AE=BD,过A作AH⊥CE于H,交BC于G.