题目内容
四边形ABCD中，∠A=90°，AD∥BC，AD=999，BC=1003，AB=2002，点P在CD上，则使∠APB=90°的点P有（ ）个．
| A、0 | B、1 | C、2 | D、无数点 |
分析：取AB，CD的中点M，N，连接MN．根据梯形中位线定理可知以AB为直径的圆与CD相交，由圆周角定理可以求解．
解答：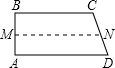
解：取AB，CD的中点M，N，连接MN．
则MN=
（AD+BC）=1001，
因为M到CD的距离小于1001，
所以，以AB为直径的圆与CD相交，
故存在两个点（即圆与CD交点），使∠APB=90°．
故选C．
解：取AB，CD的中点M，N，连接MN．则MN=
| 1 |
| 2 |
因为M到CD的距离小于1001，
所以，以AB为直径的圆与CD相交，
故存在两个点（即圆与CD交点），使∠APB=90°．
故选C．
点评：本题考查了直线与圆的位置关系，通过作梯形中位线，得出以AB为直径的圆与CD相交是解题的关键．
练习册系列答案
科学实验活动册系列答案
相关题目
23、如图，四边形ABCD中，对角线AC、BD相交于点E．已知：DA=DC，E为AC中点．
如图所示，在平行四边形ABCD中，AE是∠DAB的平分线，EF∥AD交AB于点F，若AB=9，CE=4，AE=8，则DF等于（ ）
17、如图，在平行四边形ABCD中，对角线AC、BD相交于点O，过点O的直线EF分别交AB、CD于E、F．请写出图中三对全等的三角形：
7、如图，在四边形ABCD中，AD=CB，∠ACB=∠CAD．求证：AB=CD．