Question

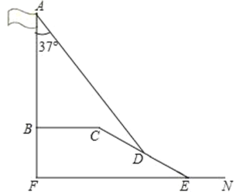
【题目】在学习解直角三角形以后，重庆八中数学兴趣小组测量了旗杆的高度，如图，某一时刻，旗杆AB的影子一部分落在平台上，另一部分落在斜坡上，测得落在平台上的影长BC为6米，落在斜坡上的影长CD为4米，AB⊥BC，同一时刻，光线与旗杆的夹角为37°，斜坡CE的坡角为30°，旗杆的高度约为多少米？（结果精确到0.1，参考数据：sin37°＝0.60，cos37°≈0.80，tan37°≈0.75，≈1.73）

Answer 1

【答案】10.6

【解析】

通过作垂线把特殊角放在直角三角形中，利用三角函数由边求边，即由PH求AP，由DQ可求出QH，最后AP+PB=AB求出旗杆高度.

解：如图，过点C作CG⊥EF于点G，延长GH交AD于点H，过点H作HP⊥AB于点P，

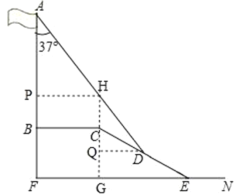
则四边形BCHP为矩形，

∴BC＝PH＝6，BP＝CH，∠CHD＝∠A＝37°，

∴AP= = =8

过点D作DQ⊥GH于点Q，

∴∠CDQ＝∠CEG＝30°，

∴CQ= CD=2，DQ=CDcos∠CDQ=4×=2 ，
∵QH= == ，
∴CH=QH﹣CQ=﹣2，
则AB=AP+PB=AP+CH=8+-2≈10.6，