题目内容
如图,已知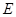 、
、 分别是平行四边形
分别是平行四边形 的边
的边 、
、 上的两点,且
上的两点,且  .
.
(1)求证: ;
;
(2)判定四边形 是否是平行四边形?
是否是平行四边形?
可通过证明 ,
, ,又
,又 ,
,  (2)四边形
(2)四边形 是平行四边形.
是平行四边形.
解析试题分析:(1)证明: 四边形
四边形 为平行四边形,
为平行四边形,  ,
, .
.
又 ,
,  .
.
(2) ,又由
,又由 知
知 ,
, ,即
,即 .
. 四边形
四边形 是平行四边形.
是平行四边形.
考点:平行四边形判定及性质
点评:本题难度中等,主要考查学生对平行四边形判定及性质及全等三角形知识点的掌握,为中考常考题型,要求学生牢固掌握解题技巧。

练习册系列答案
相关题目
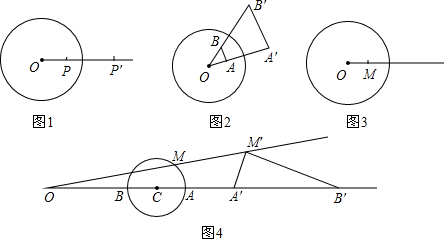
(12分)如图1,在平面上,给定了半径为 的⊙
的⊙ ,对于任意点
,对于任意点 ,在射线
,在射线 上取一点
上取一点 ,使得
,使得 ·
· =
= ,这种把点
,这种把点 变为点
变为点 的变换叫做反演变换,点
的变换叫做反演变换,点 与点
与点 叫做互为反演点,⊙
叫做互为反演点,⊙ 称为基圆.
称为基圆.

⑴如图2,⊙ 内有不同的两点
内有不同的两点 、
、 ,它们的反演点分别是
,它们的反演点分别是 、
、 ,则与∠
,则与∠ 一定相等的角是( ▲ )
一定相等的角是( ▲ )
⑵如图3,⊙ 内有一点
内有一点 ,请用尺规作图画出点
,请用尺规作图画出点 的反演点
的反演点 ;(保留画图痕迹,不必写画法).
;(保留画图痕迹,不必写画法).
⑶如果一个图形上各点经过反演变换得到的反演点组成另一个图形,那么这两个图形叫做互为反演图形.已知基圆 的半径为
的半径为 ,另一个半径为
,另一个半径为 的⊙
的⊙ ,作射线
,作射线 交⊙
交⊙ 于点
于点 、
、 ,点
,点 、
、 关于⊙
关于⊙ 的反演点分别是
的反演点分别是 、
、 ,点
,点 为⊙
为⊙ 上另一点,关于⊙
上另一点,关于⊙ 的反演点为
的反演点为 .求证:∠
.求证:∠ =90°.
=90°.
 的⊙
的⊙ ,对于任意点
,对于任意点 ,在射线
,在射线 上取一点
上取一点 ,使得
,使得 ·
· =
= ,这种把点
,这种把点 变为点
变为点 的变换叫做反演变换,点
的变换叫做反演变换,点 与点
与点 叫做互为反演点,⊙
叫做互为反演点,⊙ 称为基圆.
称为基圆.
⑴如图2,⊙
 内有不同的两点
内有不同的两点 、
、 ,它们的反演点分别是
,它们的反演点分别是 、
、 ,则与∠
,则与∠ 一定相等的角是( ▲ )
一定相等的角是( ▲ )A.∠ | B.∠ | C.∠ | D.∠ |
 内有一点
内有一点 ,请用尺规作图画出点
,请用尺规作图画出点 的反演点
的反演点 ;(保留画图痕迹,不必写画法).
;(保留画图痕迹,不必写画法).⑶如果一个图形上各点经过反演变换得到的反演点组成另一个图形,那么这两个图形叫做互为反演图形.已知基圆
 的半径为
的半径为 ,另一个半径为
,另一个半径为 的⊙
的⊙ ,作射线
,作射线 交⊙
交⊙ 于点
于点 、
、 ,点
,点 、
、 关于⊙
关于⊙ 的反演点分别是
的反演点分别是 、
、 ,点
,点 为⊙
为⊙ 上另一点,关于⊙
上另一点,关于⊙ 的反演点为
的反演点为 .求证:∠
.求证:∠ =90°.
=90°.
(12分)如图1,在平面上,给定了半径为 的⊙
的⊙ ,对于任意点
,对于任意点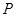 ,在射线
,在射线 上取一点
上取一点 ,使得
,使得 ·
· =
= ,这种把点
,这种把点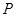 变为点
变为点 的变换叫做反演变换,点
的变换叫做反演变换,点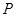 与点
与点 叫做互为反演点,⊙
叫做互为反演点,⊙ 称为基圆.
称为基圆.
⑴如图2,⊙ 内有不同的两点
内有不同的两点 、
、 ,它们的反演点分别是
,它们的反演点分别是 、
、 ,则与∠
,则与∠ 一定相等的角是( ▲ )
一定相等的角是( ▲ )
A.∠ | B.∠ | C.∠ | D.∠ |
 内有一点
内有一点 ,请用尺规作图画出点
,请用尺规作图画出点 的反演点
的反演点 ;(保留画图痕迹,不必写画法).
;(保留画图痕迹,不必写画法).⑶如果一个图形上各点经过反演变换得到的反演点组成另一个图形,那么这两个图形叫做互为反演图形.已知基圆
 的半径为
的半径为 ,另一个半径为
,另一个半径为 的⊙
的⊙ ,作射线
,作射线 交⊙
交⊙ 于点
于点 、
、 ,点
,点 、
、 关于⊙
关于⊙ 的反演点分别是
的反演点分别是 、
、 ,点
,点 为⊙
为⊙ 上另一点,关于⊙
上另一点,关于⊙ 的反演点为
的反演点为 .求证:∠
.求证:∠ =90°.
=90°.

 (C)∠
(C)∠ (D)∠
(D)∠
 =90°.
=90°.
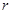 的⊙
的⊙ ,对于任意点
,对于任意点 ,在射线
,在射线 上取一点
上取一点 ,使得
,使得 =
= ,这种把点
,这种把点
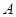 、
、 ,它们的反演点分别是
,它们的反演点分别是 、
、 ,则与∠
,则与∠ (C)∠
(C)∠ (D)∠
(D)∠ ,请用尺规作图画出点
,请用尺规作图画出点 ;(保留画图痕迹,不必写画法).
;(保留画图痕迹,不必写画法). 的⊙
的⊙ ,作射线
,作射线 交⊙
交⊙ =90°.
=90°.