题目内容
 如图,小勇要用长20m的铁栏杆,一面靠墙AD,围成一个矩形的花圃(墙足够长).求AB的长为多少时,花圃的面积最大?并求出这个最大面积.
如图,小勇要用长20m的铁栏杆,一面靠墙AD,围成一个矩形的花圃(墙足够长).求AB的长为多少时,花圃的面积最大?并求出这个最大面积.分析:设AB=xm,花圃的面积为ym2,根据矩形的面积公式可以得到关于x的二次函数,接着利用二次函数的性质即可求解.
解答:解:设AB=xm,花圃的面积为ym2,
则有y=x(20-2x),
即y=-2x2+20x ( 0<x<10),
∴顶点坐标是(5,50).
当x=5时,函数取得最大值50,.
故AB为5m时,花圃的面积最大,这个最大面积为50m2.
则有y=x(20-2x),
即y=-2x2+20x ( 0<x<10),
∴顶点坐标是(5,50).
当x=5时,函数取得最大值50,.
故AB为5m时,花圃的面积最大,这个最大面积为50m2.
点评:此题主要考查了二次函数的应用,最大面积的问题常利函数的增减性来解答,我们首先要吃透题意,确定变量,建立函数模型,然后结合实际选择最优方案.其中要注意应该在自变量的取值范围内求最大值(或最小值),也就是说二次函数的最值不一定在x=-
时取得.
| b |
| 2a |

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
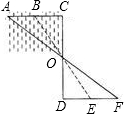 如图,小勇要测量家门前河中浅滩B到对岸A的距离,先在岸边定出C点,使C,A,B在同一直线上,再依AC的垂直方向在岸边画CD,取它的中点O,又画DF⊥CD,观测得到E,O,B在同一直线上,且F,O,A也在同一直线上,那么EF的长就是浅滩B和对岸A的距离,你能说出这是为什么吗?
如图,小勇要测量家门前河中浅滩B到对岸A的距离,先在岸边定出C点,使C,A,B在同一直线上,再依AC的垂直方向在岸边画CD,取它的中点O,又画DF⊥CD,观测得到E,O,B在同一直线上,且F,O,A也在同一直线上,那么EF的长就是浅滩B和对岸A的距离,你能说出这是为什么吗?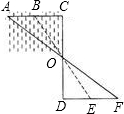 如图,小勇要测量家门前河中浅滩B到对岸A的距离,先在岸边定出C点,使C,A,B在同一直线上,再依AC的垂直方向在岸边画CD,取它的中点O,又画DF⊥CD,观测得到E,O,B在同一直线上,且F,O,A也在同一直线上,那么EF的长就是浅滩B和对岸A的距离,你能说出这是为什么吗?
如图,小勇要测量家门前河中浅滩B到对岸A的距离,先在岸边定出C点,使C,A,B在同一直线上,再依AC的垂直方向在岸边画CD,取它的中点O,又画DF⊥CD,观测得到E,O,B在同一直线上,且F,O,A也在同一直线上,那么EF的长就是浅滩B和对岸A的距离,你能说出这是为什么吗? 如图,小勇要用长20m的铁栏杆,一面靠墙AD,围成一个矩形的花圃(墙足够长).求AB的长为多少时,花圃的面积最大?并求出这个最大面积.
如图,小勇要用长20m的铁栏杆,一面靠墙AD,围成一个矩形的花圃(墙足够长).求AB的长为多少时,花圃的面积最大?并求出这个最大面积.