Question

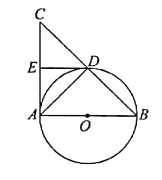
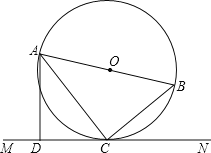
【题目】如图所示，矩形中，，，点在上，.动点、分别从点、同时出发，沿射线、线段向点的方向运动（点可运动到的延长线上），当动点运动到点时，、两点同时停止运动.联结、、，过三边的中点作.设动点、的速度都是1个单位/秒，、运动的时间为秒.试解答下列问题：

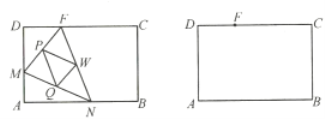
（1）说明；

（2）设，试问为何值时，为直角三角形？

（3）试用含的代数式表示，并求当为何值时，最小？求此时的值.

Answer 1

【答案】（1）见解析；（2）当或时，为直角三角形；（3）当时， 的值最小，；当时，的值也最小，.

【解析】

（1）由根据题意可知P、W、Q分别是△FMN三边的中点，可得PW是△FMN的中位线，然后即可证明△FMN∽△QWP；

（2）由（1）得，△FMN∽△QWP，当△QWP为直角三角形时，△FMN为直角三角形，根据DM＝BN＝x，AN＝6x，AM＝4x，利用勾股定理求得FM2＝4＋x2，MN2＝（4x）2＋（6x）2，FN2＝（4x）2＋16，然后分①当MN2＝FM2＋FN2时，②当FN2＝FM2＋MN2时，③FM2＝MN2＋FN2时三种情况讨论即可．

（3）根据①当0≤x≤4，即M从D到A运动时，MN≥AN，AN＝6x，故只有当x＝4时，MN的值最小即可求得答案，②当4＜x≤6时，MN2＝AM2＋AN2＝（x4）2＋（6x）2，解得x即可.

（1）由题意可知、、分别是三边的中点，

是的中位线，即，

同理，.

，

同理，.

（2）由（1）得，，

故当为直角三角形时，为直角三角形，

反之亦然.

由题意可得，，，

由勾股定理分别得，，.

过点N作NK⊥CD于K，

∴CK＝BN＝x，

∵CF＝CDDF＝62＝4，

∴FK＝4x，

∴FN2＝NK2＋FK2＝（4x）2＋16，

①当MN2＝FM2＋FN2时，（4x）2＋（6x）2＝4＋x2＋（4x）2＋16，

解得x＝，

②当时，，

此方程无实数根.

③时，，

解得（不合题意，舍去），，

综上，当或时，为直角三角形

（3）①当，即从到运动时，，，

故只有当时，的最小值，的值也最小，

此时，；

②当时，，

当，取得最小值2，

当时，的值最小，此时.

综上：当时， 的值最小，；当时，的值也最小，.