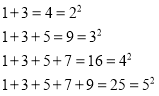题目内容
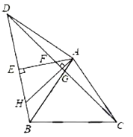
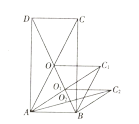
【题目】如图,矩形![]() 的面积为20cm2,对角线交于点
的面积为20cm2,对角线交于点![]() ,以AB、AO为邻边作平行四边形
,以AB、AO为邻边作平行四边形![]() ,对角线交于点
,对角线交于点![]() ;以
;以![]() 为邻边作平行四边形
为邻边作平行四边形![]() ;…;依此类推,则平行四边形
;…;依此类推,则平行四边形![]() 的面积为______,平行四边形
的面积为______,平行四边形![]() 的面积为______.
的面积为______.
【答案】![]()
![]()
【解析】
根据矩形的性质求出△AOB的面积等于矩形ABCD的面积的![]() ,求出△AOB的面积,再分别求出△ABO1、△ABO2、△ABO3、△ABO4的面积,求出平行四边形
,求出△AOB的面积,再分别求出△ABO1、△ABO2、△ABO3、△ABO4的面积,求出平行四边形![]() 的面积,然后再观察发现规律进行解答.
的面积,然后再观察发现规律进行解答.

解:∵四边形ABCD是矩形,
∴AO=CO,BO=DO,DC∥AB,DC=AB,
∴S△ADC=S△ABC=![]() S矩形ABCD=
S矩形ABCD=![]() ×20=10,
×20=10,
∴S△AOB=S△BCO=![]() S△ABC=
S△ABC=![]() ×10=5,
×10=5,
∴S△ABO1=![]() S△AOB=
S△AOB=![]() ×5=
×5=![]() ,
,
∴S△ABO2=![]() S△ABO1=
S△ABO1=![]() ,
,
S△ABO3=![]() S△ABO2=
S△ABO2=![]() ,
,
S△ABO4=![]() S△ABO3=
S△ABO3=![]() ,
,
∴S平行四边形AO4C5B=2S△ABO4=2×![]() =
=![]() ,
,
∴平行四边形![]() 的面积为:,
的面积为:,
故答案为:![]() ,
,![]() .
.

 阅读快车系列答案
阅读快车系列答案【题目】某校八年级两个班各选派10名学生参加“垃圾分类知识竞赛,各参赛选手的成绩如下:
八(1)班:88,91,92,93,93,93,94,98,98,100;
八(2)班:89,93,93,93,95,96,96,98,98,99
通过整理,得到数据分析表如下
班级 | 最高分 | 平均分 | 中位数 | 众数 | 方差 |
八(1)班 | 100 |
| 93 | 93 | 12 |
八(2)班 | 99 | 95 |
|
| 8.4 |
(1)求表中![]() ,
,![]() ,
,![]() 的值;
的值;
(2)依据数据分析表,有同学认为最高分在(1)班,(1)班的成绩比(2)班好.但也有同学认为(2)班的成绩更好.请你写出两条支持八(2)班成绩更好的理由.
【题目】如图①,在正方形ABCD中,![]() ,点E,F分别在BC、CD上,
,点E,F分别在BC、CD上,![]() ,试探究
,试探究![]() 面积的最小值。
面积的最小值。
下面是小丽的探究过程:
(1)延长EB至G,使![]() ,连接AG,可以证明
,连接AG,可以证明![]() .请完成她的证明;
.请完成她的证明;
(2)设![]() ,
,![]() ,
,![]()
①结合(1)中结论,通过计算得到![]() 与x的部分对应值。请求出表格中a的值:(写出解答过程)
与x的部分对应值。请求出表格中a的值:(写出解答过程)
x | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 10 | 8.18 | 6.67 | 5.38 | 4.29 | 3.33 | a | 1.76 | 1.11 | 0.53 | 0 |
②利用上表和(1)中的结论通过描点、连线可以分别画出函数![]() 、
、![]() 的图像、请在图②中完善她的画图;
的图像、请在图②中完善她的画图;
③根据以上探究,估计![]() 面积的最小值约为(结果估计到0.1)。
面积的最小值约为(结果估计到0.1)。


图① 图②