题目内容
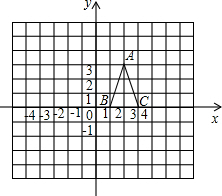 如图,△ABC的三个顶点坐标分别为A(2,3)、B(1,0)、C(3,0),把△ABC沿x轴负方向平移5个单位,得到△A′B′C′(顶点对应关系:A→A′B→B′C→C′)
如图,△ABC的三个顶点坐标分别为A(2,3)、B(1,0)、C(3,0),把△ABC沿x轴负方向平移5个单位,得到△A′B′C′(顶点对应关系:A→A′B→B′C→C′)
(1)在右图坐标系中作出△A′B′C′.
(2)连接点A、点B′,求线段A B′的长.
(3)求线段A B′所在直线的函数解析式.
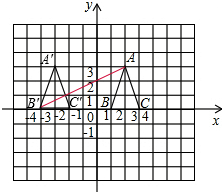 解:(1)如图所示;
解:(1)如图所示;(2)根据勾股定理,AB′=
 =
= ;
;(3)设直线AB′的函数解析式为y=kx+b,
把A(2,3)、B(-4,0)分别代入上式:
 ,
,解得,
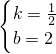 ,
,所以,直线AB′的解析式为y=
 x+2.
x+2.分析:(1)根据网格结构找出点A′、B′、C′的位置,然后顺次连接即可;
(2)在网格结构中,利用勾股定理列式计算即可得解;
(3)利用待定系数法求直线解析式解答.
点评:本题考查了利用平移变换作图,待定系数法求直线解析式,熟悉网格结构,准确找出对应点的位置是解题的关键.

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目
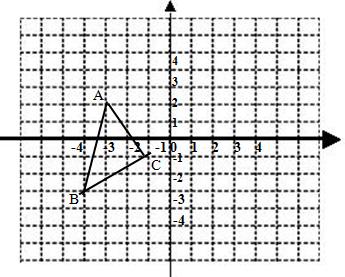
 22、已知:如图,△ABC的三个顶点都在格点上,直线l1和l2互相垂直,且相交于O.
22、已知:如图,△ABC的三个顶点都在格点上,直线l1和l2互相垂直,且相交于O. 如图,△ABC的三个顶点都在格点上.
如图,△ABC的三个顶点都在格点上. (2013•遂宁)如图,△ABC的三个顶点都在5×5的网格(每个小正方形的边长均为1个单位长度)的格点上,将△ABC绕点B逆时针旋转到△A′BC′的位置,且点A′、C′仍落在格点上,则图中阴影部分的面积约是
(2013•遂宁)如图,△ABC的三个顶点都在5×5的网格(每个小正方形的边长均为1个单位长度)的格点上,将△ABC绕点B逆时针旋转到△A′BC′的位置,且点A′、C′仍落在格点上,则图中阴影部分的面积约是 如图,△ABC的三个顶点分别在格子的3个顶点上,请你试着再在格子的顶点上找出一个点D,使得△DBC与△ABC全等,把这样的三角形都画出来.
如图,△ABC的三个顶点分别在格子的3个顶点上,请你试着再在格子的顶点上找出一个点D,使得△DBC与△ABC全等,把这样的三角形都画出来.