题目内容
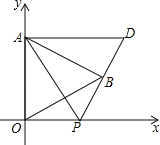
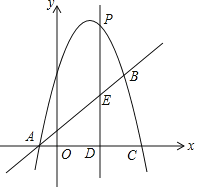
【题目】如图,抛物线![]() 与直线
与直线![]() 相交于
相交于![]() ,
,![]() 两点,且抛物线经过点
两点,且抛物线经过点![]() .
.
![]() 求抛物线的解析式;
求抛物线的解析式;
![]() 点P是抛物线上的一个动点
点P是抛物线上的一个动点![]() 不与点A、点B重合
不与点A、点B重合![]() ,过点P作直线
,过点P作直线![]() 轴于点D,交直线AB于点E.
轴于点D,交直线AB于点E.
![]() 当
当![]() 时,求P点坐标;
时,求P点坐标;
![]() 是否存在点P使
是否存在点P使![]() 为等腰三角形?若存在请直接写出点P的坐标;若不存在,请说明理由.
为等腰三角形?若存在请直接写出点P的坐标;若不存在,请说明理由.
【答案】(1)![]() (2)点P坐标为
(2)点P坐标为![]() 或
或![]() 或
或![]() 或
或![]() .
.
【解析】分析:(1)由直线解析式可求得B点坐标,由A、B、C三点的坐标,利用待定系数法可求得抛物线解析式;
(2)①可设出P点坐标,则可表示出E、D的坐标,从而可表示出PE和ED的长,由条件可知到关于P点坐标的方程,则可求得P点坐标;②由E、B、C三点坐标可表示出BE、CE和BC的长,由等腰三角形的性质可得到关于E点坐标的方程,可求得E点坐标,则可求得P点坐标.
详解:![]() 点
点![]() 在直线
在直线![]() 上,
上,
![]() ,
,
![]() ,
,
把A、B、C三点坐标代入抛物线解析式可得 ,解得
,解得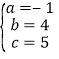 ,
,
![]() 抛物线解析式为
抛物线解析式为![]() ;
;
![]() 设
设![]() ,则
,则![]() ,
,![]() ,
,
则![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
当![]() 时,解得
时,解得![]() 或
或![]() ,但当
,但当![]() 时,P与A重合不合题意,舍去,
时,P与A重合不合题意,舍去,
![]() ;
;
当![]() 时,解得
时,解得![]() 或
或![]() ,但当
,但当![]() 时,P与A重合不合题意,舍去,
时,P与A重合不合题意,舍去,
![]() ;
;
综上可知P点坐标为![]() 或
或![]() ;
;
![]() 设
设![]() ,则
,则![]() ,且
,且![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() ,
,
当![]() 为等腰三角形时,则有
为等腰三角形时,则有![]() 、
、![]() 或
或![]() 三种情况,
三种情况,
当![]() 时,则
时,则![]() ,解得
,解得![]() ,此时P点坐标为
,此时P点坐标为![]() ;
;
当![]() 时,则
时,则![]() ,解得
,解得![]() 或
或![]() ,此时P点坐标为
,此时P点坐标为![]() 或
或![]() ;
;
当![]() 时,则
时,则![]() ,解得
,解得![]() 或
或![]() ,当
,当![]() 时E点与B点重合,不合题意,舍去,此时P点坐标为
时E点与B点重合,不合题意,舍去,此时P点坐标为![]() ;
;
综上可知存在满足条件的点P,其坐标为![]() 或
或![]() 或
或![]() 或
或![]() .
.

【题目】某超市销售一种商品,每件的成本每千克18元,规定每千克售价不低于成本,且获利不得高于100%,经市场调查,每天的销售量y(千克)与每千克售价x(元)满足一次函数关系,部分数据如下表:
售价x(元/千克) | 40 | 39 | 38 | 37 |
销售量y(千克) | 20 | 22 | 24 | 26 |
(1)求y与x之间的函数表达式;
(2)设商品每天的总利润为W(元),求W与x之间的函数表达式(利润=收入﹣成本),并指出售价为多少元时获得最大利润,最大利润是多少?
(3)该超市若想每天销售利润不低于480元,请结合函数图象帮助超市确定产品的销售单价范围?