��Ŀ����
���Ķ�����֪ʶ��Ȼ���������������⣺
����һ��δ֪��������δ֪������ߴ�ָ����2�ķ��̣�����һԪ���η��̣��磺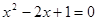 .
.
���ǰ�����һ����ʽ������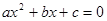 (a��b��c��ʾ��֪����
(a��b��c��ʾ��֪����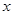 ��δ֪����a��0)�����Ľ������ǣ�
��δ֪����a��0)�����Ľ������ǣ�
�� ��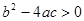 ʱ����������������ȵĽ⣻
ʱ����������������ȵĽ⣻
�� ��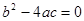 ʱ��������������ȵĽ⣨��һ���⣩��
ʱ��������������ȵĽ⣨��һ���⣩��
�� ��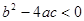 ʱ������û�н⣻
ʱ������û�н⣻
��1��һԪ���η���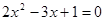 �м����⣿Ϊʲô��
�м����⣿Ϊʲô��
��2����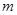 ȡ��ֵʱ������
ȡ��ֵʱ������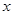 ��һԪ���η���
��һԪ���η���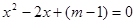 û�н⣿
û�н⣿
����һ��δ֪��������δ֪������ߴ�ָ����2�ķ��̣�����һԪ���η��̣��磺
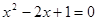 .
.���ǰ�����һ����ʽ������
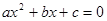 (a��b��c��ʾ��֪����
(a��b��c��ʾ��֪����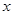 ��δ֪����a��0)�����Ľ������ǣ�
��δ֪����a��0)�����Ľ������ǣ��� ��
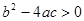 ʱ����������������ȵĽ⣻
ʱ����������������ȵĽ⣻�� ��
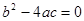 ʱ��������������ȵĽ⣨��һ���⣩��
ʱ��������������ȵĽ⣨��һ���⣩���� ��
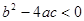 ʱ������û�н⣻
ʱ������û�н⣻��1��һԪ���η���
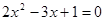 �м����⣿Ϊʲô��
�м����⣿Ϊʲô����2����
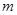 ȡ��ֵʱ������
ȡ��ֵʱ������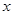 ��һԪ���η���
��һԪ���η���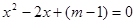 û�н⣿
û�н⣿��1������������ȵ�ʵ������
��2x2-3x+1=0��a=2��b=--3��c=1��
���=b2-4ac=��-3��2-4��2��1=-1��0��
�������������ȵ�ʵ������
��2����x2-2x+��m-1��=0��a=1��b=-2��c=m-1��
���=b2-4ac=��-2��2-4��1����m-1��=8-4m��0��
���m��2��
��m��2������x��һԪ���η���x2-2x+��m-1��=0�⣮
��2x2-3x+1=0��a=2��b=--3��c=1��
���=b2-4ac=��-3��2-4��2��1=-1��0��
�������������ȵ�ʵ������
��2����x2-2x+��m-1��=0��a=1��b=-2��c=m-1��
���=b2-4ac=��-2��2-4��1����m-1��=8-4m��0��
���m��2��
��m��2������x��һԪ���η���x2-2x+��m-1��=0�⣮
����������б�ʽ��=b2-4ac��ֵ�ķ��žͿ����жϸ��������

��ϰ��ϵ�д�
�����Ŀ
 .
. ��
�� ����ϵ��
����ϵ�� ��
�� ����1��2��3��4��5��ȡֵ����������ʵ����ķ��̵ĸ����� ��
����1��2��3��4��5��ȡֵ����������ʵ����ķ��̵ĸ����� �� ��
�� 


 �������ʽ
�������ʽ ��ֵ��
��ֵ��