Question

【题目】如图所示，边长为2的正三角形ABO的边OB在x轴上，将△ABO绕原点O逆时针旋转30°得到三角形OA1B1 ， 则点A1的坐标为（ ）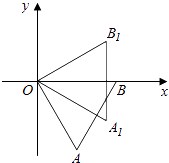

A.（ ，1）
B.（ ，-1）
C.（-1， ）
D.（2，1）

Answer 1

【答案】B
【解析】如图，设A1B1与x轴相交于C，

∵△ABO是等边三角形，旋转角为30°，

∴∠A1OC=60°-30°=30°，

∴A1B1⊥x轴，

∵等边△ABO的边长为2，

∴OC= ×2= ，

A1C= ×2=1，

又∵A1在第四象限，

∴点A1的坐标为（ ，-1）．

故答案为：B．

由旋转角相等易得=30°，∠A1OC=60°-30°=30°再利用30°所对直角边等于斜边的一半，结合勾股定理容易算出OC，A1C的长，进而得到点A1的坐标