题目内容
 菱形OABC在平面直角坐标系中的位置如图所示.∠AOC=45°,OC=
菱形OABC在平面直角坐标系中的位置如图所示.∠AOC=45°,OC= ,则点B的坐标为( )
,则点B的坐标为( )A.(
 ,1)
,1)B.(1,
 )
)C.(
 +1,1)
+1,1)D.(1,
 +1)
+1)
【答案】分析:根据菱形的性质,作CD⊥x轴,先求C点坐标,然后求得点B的坐标.
解答: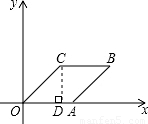 解:作CD⊥x轴于点D,
解:作CD⊥x轴于点D,
∵四边形OABC是菱形,OC=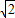 ,
,
∴OA=OC=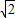 ,
,
又∵∠AOC=45°
∴△OCD为等腰直角三角形,
∵OC=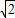 ,
,
∴OD=CD=OC×sin∠COD=OC×sin45°=1,
则点C的坐标为(1,1),
又∵BC=OA=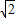 ,
,
∴B的横坐标为OD+BC=1+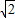 ,B的纵坐标为CD=1,
,B的纵坐标为CD=1,
则点B的坐标为(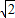 +1,1).
+1,1).
故选C.
点评:本题综合考查了图形的性质和坐标的确定,综合性较强.
解答:
 解:作CD⊥x轴于点D,
解:作CD⊥x轴于点D,∵四边形OABC是菱形,OC=
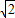 ,
,∴OA=OC=
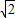 ,
,又∵∠AOC=45°
∴△OCD为等腰直角三角形,
∵OC=
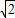 ,
,∴OD=CD=OC×sin∠COD=OC×sin45°=1,
则点C的坐标为(1,1),
又∵BC=OA=
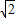 ,
,∴B的横坐标为OD+BC=1+
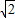 ,B的纵坐标为CD=1,
,B的纵坐标为CD=1,则点B的坐标为(
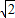 +1,1).
+1,1).故选C.
点评:本题综合考查了图形的性质和坐标的确定,综合性较强.

练习册系列答案
相关题目
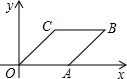 菱形OABC在平面直角坐标系中的位置如图所示.∠AOC=45°,OC=
菱形OABC在平面直角坐标系中的位置如图所示.∠AOC=45°,OC= (2013•瑶海区一模)每个小方格是边长为1个单位长度的小正方形,菱形OABC在平面直角坐标系的位置如图所示.
(2013•瑶海区一模)每个小方格是边长为1个单位长度的小正方形,菱形OABC在平面直角坐标系的位置如图所示. 秒
秒 如图,菱形OABC在平面直角坐标系中的位置如图所示,∠AOC=45°,OC=
如图,菱形OABC在平面直角坐标系中的位置如图所示,∠AOC=45°,OC=