题目内容
【题目】如图,Rt△ABC中∠C=90°,∠BAC=30°,AB=8,以2![]() 为边长的正方形DEFG的一边GD在直线AB上,且点D与点A重合,现将正方形DEFG沿A﹣B的方向以每秒1个单位的速度匀速运动,当点D与点B重合时停止,则在这个运动过程中,正方形DEFG与△ABC的重合部分的面积S与运动时间t之间的函数关系图象大致是( )
为边长的正方形DEFG的一边GD在直线AB上,且点D与点A重合,现将正方形DEFG沿A﹣B的方向以每秒1个单位的速度匀速运动,当点D与点B重合时停止,则在这个运动过程中,正方形DEFG与△ABC的重合部分的面积S与运动时间t之间的函数关系图象大致是( )

A. 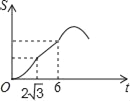 B.
B. 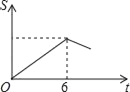 C.
C. 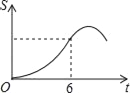 D.
D. 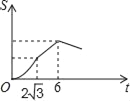
【答案】A
【解析】解:如图1,CH是AB边上的高,与AB相交于点H,,∵∠C=90°,∠BAC=30°,AB=8,∴AC=AB×cos30°=8×![]() =
=![]() ,BC=AB×sin30°=8×
,BC=AB×sin30°=8×![]() =4,∴CH=AC×BC÷AB=
=4,∴CH=AC×BC÷AB=![]() ×4÷8=
×4÷8=![]() ,AH=
,AH= ![]() ÷AB=
÷AB=![]() ;
;
(1)当0≤t≤![]() 时,S=
时,S=![]() =
=![]() ;
;

(2)当![]() 时,S=
时,S=![]() =
=![]() ;
;
(3)当6<t≤8时,S=![]()
=![]() ;
;
综上,可得:
S= ,
,
∴正方形DEFG与△ABC的重合部分的面积S与运动时间t之间的函数关系图象大致是A图象.故选A.

练习册系列答案
 春雨教育同步作文系列答案
春雨教育同步作文系列答案
相关题目