题目内容
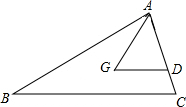如图，点G是△ABC的重心，GD∥BC，则SADG：S△ABC等于
- A.2：3
- B.4：9
- C.2：9
- D.无法确定
C
分析：根据重心的性质得出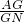
=
，以及
=
，即可得出SADG：S△ANC的比值，再利用三角形中线的性质得出S△ANC=S△ABN，进而得出答案．
解答：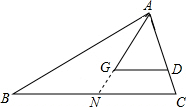
解：延长AG到BC于点N，
∵点G是△ABC的重心，GD∥BC，
∴=，
∴=，
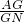∴SADG：S△ANC=（）2=
，
∵根据G是△ABC的重心，则AN是三角形中线，
∴S△ANC=S△ABN，
∴SADG：S△ABC=4：18=2：9．
故选：C．
点评：此题主要考查了相似三角形的判定与性质和三角形重心的性质等知识，根据已知得出SADG：S△ANC=（）2是解题关键．
分析：根据重心的性质得出
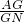=，以及=，即可得出SADG：S△ANC的比值，再利用三角形中线的性质得出S△ANC=S△ABN，进而得出答案．解答：
解：延长AG到BC于点N，∵点G是△ABC的重心，GD∥BC，
∴
=，∴
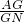=，∴SADG：S△ANC=（
）2=，∵根据G是△ABC的重心，则AN是三角形中线，
∴S△ANC=S△ABN，
∴SADG：S△ABC=4：18=2：9．
故选：C．
点评：此题主要考查了相似三角形的判定与性质和三角形重心的性质等知识，根据已知得出SADG：S△ANC=（
）2是解题关键． 
练习册系列答案
相关题目
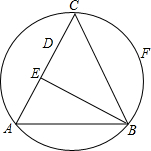如图，点F是△ABC外接圆
27、如图，点P是△ABC内的一点，有下列结论：①∠BPC＞∠A；②∠BPC一定是钝角；③∠BPC=∠A+∠ABP+∠ACP．其中正确的结论共有（ ）
如图，点O是△ABC内任意一点，G、D、E分别为AC、OA、OB的中点，F为BC上一动点，问四边形GDEF能否为平行四边形？若可以，指出F点位置，并给予证明．
（2013•攀枝花模拟）如图，点G是△ABC的重心，CG的延长线交AB于D，GA=5，GC=4，GB=3，将△ADG绕点D顺时针方向旋转180°得到△BDE，则△EBC的面积=
（1997•天津）如图，点I是△ABC的内心，AI交BC边于D，交△ABC的外接圆于点E．