题目内容
18.已知点P是正方形ABCD所在平面内一点,且△PCD为正三角形,则△APB的度数是( )| A. | 30° | B. | 150° | C. | 15°或150° | D. | 30°或150° |
分析 分两种情况:
①当点P在正方形ABCD的内部时,如图1,先根据△PCD为正三角形,得∠DPC=60°,再由等腰三角形的性质求∠APD=∠BPC=75°,最后利用周角360°求差得出∠APB的度数;
②当点P在正方形ABCD的外部时,如图2,同理可得∠APB=30°.
解答  解:分两种情况:
解:分两种情况:
①当点P在正方形ABCD的内部时,如图1,
∵△PCD为正三角形,
∴∠DPC=∠PDC=∠PCD=60°,PD=DC,
∵四边形ABCD是正方形,
∴∠ADC=∠BCD=90°,AD=DC,
∴∠ADP=90°-60°=30°,AD=PD,
∴∠DAP=∠APD=$\frac{180-30}{2}$=75°,
同理得:∠BPC=75°,
∴∠APB=360°-∠APD-∠BPC-∠DPC=360°-75°-75°-60°=150°;
②当点P在正方形ABCD的外部时,如图2,
同理得:∠DPC=60°,
∵∠ADP=90°+60°=150°,
∵AD=PD,
∴∠DAP=∠DPA=15°,
同理∠BPC=15°,
∴∠APB=∠DPC-∠DPA-∠BPC=60°-15°-15°=30°,
综上所述,∠APB的度数是30°或150°;
故选D.
点评 本题考查了正方形的性质、等腰三角形、等边三角形的性质,熟知等边三角形各边都相等,且每一个角都是60°,明确等边对等角,利用三角形的内角和依次求出各角的度数;注意点P的不确定性,分两种情况画图,得出结论.

练习册系列答案
相关题目
9.已知代数式x-3y的值是3,则代数式2x-6y+3的值是( )
| A. | 3 | B. | 9 | C. | 7 | D. | 不能确定 |
 如图是一斜坡的横截面,某人沿着斜坡从P处出发,走了13米到达M处,此时在铅垂方向上上升了5米,那么该斜坡的坡度是i=1:2.4.
如图是一斜坡的横截面,某人沿着斜坡从P处出发,走了13米到达M处,此时在铅垂方向上上升了5米,那么该斜坡的坡度是i=1:2.4. 如图,在△ADE中,已知∠DAE=100°,DC=DA,EB=EA,则∠BAC的度数为40°.
如图,在△ADE中,已知∠DAE=100°,DC=DA,EB=EA,则∠BAC的度数为40°. 小时,求m的值.
小时,求m的值.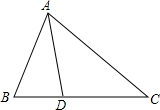 如图,已知∠BAC=60°,D是△ABC的边BC上的一点,且∠CAD=∠C,∠ADB=80°.求∠B的度数.
如图,已知∠BAC=60°,D是△ABC的边BC上的一点,且∠CAD=∠C,∠ADB=80°.求∠B的度数.