题目内容
如图,某校操场边有一棵树AB,点B、D、C在同一直线上,课间,小刚、小强和小 芳站在树边交谈.
芳站在树边交谈.
小刚说:我在D处测得树顶仰角为45°;
小强说:我在C处测得树顶仰角为30°;
小芳说:你们两人相距5m.
请你根据他们的对话,计算出该树AB的高度(结果精确到0.1米, ≈1.73).
≈1.73).
解:设AB为x米,
∵∠B=90°,∠ADB=45°,
∴BD=AB=x,
在Rt△ABC中,∠ACB=30°,tan∠ACB= ,
,
∴tan30°= =
= ,
,
解得:x≈6.8.
答:该树AB的高度约为6.8米.
分析:首先设AB为x米,由∠B=90°,∠ADB=45°,利用等腰直角三角形的性质可得:BD=AB=x,然后在Rt△ABC中,∠ACB=30°,由tan∠ACB= ,即可得方程,解此方程即可求得答案.
,即可得方程,解此方程即可求得答案.
点评:本题考查仰角的定义与解直角三角形的知识的实际应用问题.此题难度不大,解题的关键是要求学生能借助仰角构造直角三角形并解直角三角形.
∵∠B=90°,∠ADB=45°,
∴BD=AB=x,
在Rt△ABC中,∠ACB=30°,tan∠ACB=
 ,
,∴tan30°=
 =
= ,
,解得:x≈6.8.
答:该树AB的高度约为6.8米.
分析:首先设AB为x米,由∠B=90°,∠ADB=45°,利用等腰直角三角形的性质可得:BD=AB=x,然后在Rt△ABC中,∠ACB=30°,由tan∠ACB=
 ,即可得方程,解此方程即可求得答案.
,即可得方程,解此方程即可求得答案.点评:本题考查仰角的定义与解直角三角形的知识的实际应用问题.此题难度不大,解题的关键是要求学生能借助仰角构造直角三角形并解直角三角形.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目

 芳站在树边交谈.
芳站在树边交谈. ≈1.73).
≈1.73).
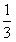 。
。
