Question

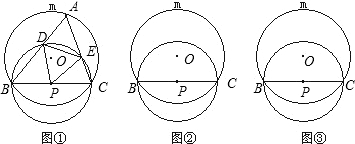
如图，⊙P与⊙O相交于A、B两点，⊙P经过圆心O，点C是⊙P的优弧上任意一点（不与点A、B重合），连接AB、AC、BC、OC．
（1）指出图中与∠ACO相等的一个角；
（2）当点C在⊙P上什么位置时，直线CA与⊙O相切？请说明理由；
（3）当∠ACB=60°时，两圆半径有怎样的大小关系？请说明你的理由．

Answer 1

【答案】分析：要使直线CA与⊙O相切，只要证得∠OAC=90°即可；根据第二问第三问就不难求得了．
解答：解：（1）连接OA，OB．
在⊙O中，∵OA=OB，
∴=，
∴∠ACO=∠BCO；

（2）连接OP，并延长与⊙P交于点D．
若点C在点D位置时，直线CA与⊙O相切
理由：连接AD，OA，则∠DAO=90°
∴OA⊥DA
∴DA与⊙O相切
即点C在点D位置时，直线CA与⊙O相切．

（3）当∠ACB=60°时，两圆半径相等；
理由：作直径OD，连接BD，AD，OA，
∵∠ADB=∠ACB=60°，PO垂直平分AB，
∴=，
∵∠ADO=∠BDO，
∴∠ADO=30°，
∵OD是直径，
∴∠DAO=90°，
∴OA=OD，
∴OA=PO，
∴当∠ACB=60°时，两圆半径相等．
点评：本题考查了等弧所对的圆周角相等、直径所对的圆周角等于90°，切线的判定等知识．具有一定的综合性和难度．