题目内容
如图，已知四条直线a，b，c，d，其中a∥b，c⊥b，且∠1=50°．则∠2=
- A.60°
- B.50°
- C.40°
- D.30°
C
分析：根据对顶角相等求出∠3，再根据垂直的定义，利用直角三角形两锐角互余求解即可．
解答：
解：∵∠1=50°，
∴∠3=∠1=50°，
∵c⊥b，
∴∠2+∠3=90°，
∴∠2=90°-50°=40°．
故选C．
点评：本题考查了对顶角相等的性质，直角三角形两锐角互余，是基础题．
分析：根据对顶角相等求出∠3，再根据垂直的定义，利用直角三角形两锐角互余求解即可．
解答：
解：∵∠1=50°，∴∠3=∠1=50°，
∵c⊥b，
∴∠2+∠3=90°，
∴∠2=90°-50°=40°．
故选C．
点评：本题考查了对顶角相等的性质，直角三角形两锐角互余，是基础题．
练习册系列答案
口算题天天练系列答案
相关题目
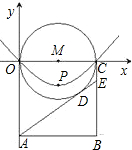立平面直角坐标系，使点B落在第四象限，一条抛物线y=ax2+bx经过O、C两点，并将抛物线的顶点记作P．
（2013•拱墅区一模）如图，已知四条直线a，b，c，d，其中a∥b，c⊥b，且∠1=50°．则∠2=（ ）
（2013•吴江市模拟）如图，已知直线l1∥l2∥l3∥l4∥l5，相邻两条平行直线间的距离相等且为1，如果四边形ABCD的四个顶点在平行直线上，∠BAD=90°且AB=3AD，DC⊥l4，则四边形ABCD的面积是（ ）